Lösung von Aufgabe 9.1P (SoSe 13): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Beweisen Sie die Halbgeradentreue der Geradenspiegelung. Nutzen Sie für den Beweis die Streckentreue der Geradenspiegelung und eine geeignete Definition des Begr…“) |
|||
| Zeile 1: | Zeile 1: | ||
Beweisen Sie die Halbgeradentreue der Geradenspiegelung. Nutzen Sie für den Beweis die Streckentreue der Geradenspiegelung und eine geeignete Definition des Begriffs Halbgerade. | Beweisen Sie die Halbgeradentreue der Geradenspiegelung. Nutzen Sie für den Beweis die Streckentreue der Geradenspiegelung und eine geeignete Definition des Begriffs Halbgerade. | ||
| + | |||
| + | |||
| + | |||
| + | {| class="wikitable" | ||
| + | | Voraussetzung || Geradenspiegelung an g <math>Sg</math> mit <math>A'= Sg (A)</math> und <math>B' = Sg (B)</math> und <math>P \in AB^{+}</math> | ||
| + | |- | ||
| + | | Behauptung || <math>Sg (AB+) = A'B'^{+}</math> d.h. <math>P' \in A'B'^{+}</math> | ||
| + | |} | ||
| + | <br /> | ||
| + | Es musshttp://upload.wikimedia.org/wikipedia/commons/f/fd/Button_underline.png also gezeigt werden, dass das Bild <math>P'</math> eines beliebigen Punkts <math>P</math> der Halbgerade auch auf dem Bilder der Halbgeraden liegt.<br /> | ||
| + | |||
| + | {| class="wikitable" | ||
| + | !Beweisschritt!!Begründung | ||
| + | |- | ||
| + | | 1 <math>P \in AB^{+}</math>|| Voraussetzung | ||
| + | |- | ||
| + | | 2 <math>P \in \ \ \overline{AB} \cup \{P|ZW (A,B,P)\} </math> || 1), Def Halbgerade | ||
| + | |- | ||
| + | | 3 <math>P \in \overline{A'B'} </math> || Streckentreue | ||
| + | |- | ||
| + | | 4 <math>P \in \overline{AB} + \overline{BP} = \overline{AP} </math> || Def Zwischen | ||
| + | |- | ||
| + | | 5 <math>P \in \overline{A'B'} + \overline{B'P'} = \overline{A'P'} </math> || Abstandserhaltung der Geradenspiegelung | ||
| + | |- | ||
| + | | 6 <math>P' \in \ \ \overline{A'B'} \cup \{P'|ZW (A',B',P')\}</math> || Def Zwischen 3), 5) | ||
| + | |- | ||
| + | | 7 <math>P' \in A'B'^{+}</math> || Def Halbgerade 6) | ||
| + | |} | ||
| + | --[[Benutzer:Regenschirm|Regenschirm]] 17:50, 25. Jun. 2013 (CEST) | ||
<br /> | <br /> | ||
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
Version vom 25. Juni 2013, 16:50 Uhr
Beweisen Sie die Halbgeradentreue der Geradenspiegelung. Nutzen Sie für den Beweis die Streckentreue der Geradenspiegelung und eine geeignete Definition des Begriffs Halbgerade.
| Voraussetzung | Geradenspiegelung an g 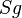 mit mit 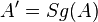 und und 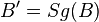 und und 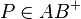
|
| Behauptung | 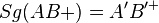 d.h. d.h. 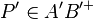
|
Es musshttp://upload.wikimedia.org/wikipedia/commons/f/fd/Button_underline.png also gezeigt werden, dass das Bild 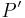 eines beliebigen Punkts
eines beliebigen Punkts  der Halbgerade auch auf dem Bilder der Halbgeraden liegt.
der Halbgerade auch auf dem Bilder der Halbgeraden liegt.
| Beweisschritt | Begründung |
|---|---|
1 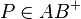 |
Voraussetzung |
2 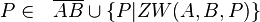 |
1), Def Halbgerade |
3 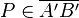 |
Streckentreue |
4 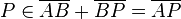 |
Def Zwischen |
5 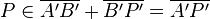 |
Abstandserhaltung der Geradenspiegelung |
6 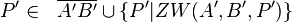 |
Def Zwischen 3), 5) |
7 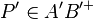 |
Def Halbgerade 6) |
--Regenschirm 17:50, 25. Jun. 2013 (CEST)

