Lösung von Aufgabe 9.1P (SoSe 13): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 35: | Zeile 35: | ||
'''Voraussetzung''':<br /> | '''Voraussetzung''':<br /> | ||
| − | AB+ ≔ {P | Zw(A,P,B) | + | AB+ ≔ {P | Zw(A,P,B) ∨ Zw(A,B,P)} ∪ {A,B}<br /> |
mit A ≠ B, A,B ∈ Ebene E<br /> | mit A ≠ B, A,B ∈ Ebene E<br /> | ||
Version vom 14. Juli 2013, 18:46 Uhr
Beweisen Sie die Halbgeradentreue der Geradenspiegelung. Nutzen Sie für den Beweis die Streckentreue der Geradenspiegelung und eine geeignete Definition des Begriffs Halbgerade.
| Voraussetzung | 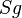 mit mit 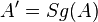 und und 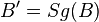 und und 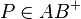
|
| Behauptung | 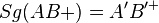 d.h. d.h. 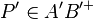
|
| Beweisschritt | Begründung |
|---|---|
1 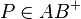 |
Voraussetzung |
2 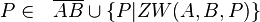 |
1), Def Halbgerade |
3 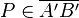 |
Streckentreue |
4 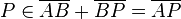 |
Def Zwischen |
5 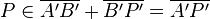 |
Abstandserhaltung der Geradenspiegelung |
6 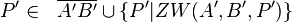 |
Def Zwischen 3), 5) |
7 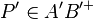 |
Def Halbgerade 6) |
--Regenschirm 17:50, 25. Jun. 2013 (CEST) Die Beweisidee und Schritte sind super. Es fehlen noch ein paar Striche und Klammern, damit der Beweis auch ganz richtig ist.--Tutorin Anne 15:18, 26. Jun. 2013 (CEST)
Voraussetzung:
AB+ ≔ {P | Zw(A,P,B) ∨ Zw(A,B,P)} ∪ {A,B}
mit A ≠ B, A,B ∈ Ebene E
A͞B := {P | Zw(A,P,B)} ∪ {A,B}
mit A ≠ B, A,B ∈ Ebene E
--Nolessonlearned 18:39, 14. Jul. 2013 (CEST)
Behauptung: AB+ ≌ A'B'+
--Nolessonlearned 18:39, 14. Jul. 2013 (CEST)
| Beweisschritt | Begründung | |
|---|---|---|
| 1) | B'= Sg(B) | Eigenschaft d. GS |
| 2) | A'= Sg(A) | Eigenschaft d. GS |
| 3) | 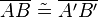
|
(1); (2); Voraussetzung; Streckentreue d. GS |
| 4) | 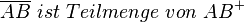
|
Voraussetzung; Def. Halbgerade |
| 5) | Fehler beim Parsen(Syntaxfehler): \overline{A'B'}\ ist\ Teilmenge\ von\ \ A'B'^{+} | (1); (2); (3); Voraussetzung; Def. Halbgerade; Streckentreue d. GS |- | 6) | <math>\\ AB^{+}\ \tilde {=} \ A'B'^{+} | (4); (5);
q.e.d. |
--Nolessonlearned 18:57, 14. Jul. 2013 (CEST)

