Lösung von Aufgabe 9.3P (SoSe 13): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(table+)
Zeile 34: Zeile 34:
 
<math>\angle ABC\ mit\ \ BA^{+}\ \cup\  \ BC^{+}\  </math>  <math>mit\ A,B,C \in\ \epsilon</math><br />
 
<math>\angle ABC\ mit\ \ BA^{+}\ \cup\  \ BC^{+}\  </math>  <math>mit\ A,B,C \in\ \epsilon</math><br />
 
<br />
 
<br />
−
'''Behauptung''': <math>\angle ABC\  \tilde {=}\ \angle A'B'C'</math>
+
'''Behauptung''': <math>\angle ABC\  \tilde {=}\ \angle A'B'C'</math><br />
 +
<br />
 +
 
 +
{| class="wikitable "
 +
|- style="background: #DDFFDD;"
 +
!
 +
! Beweisschritt
 +
! Begründung
 +
|-
 +
| 1)
 +
| A' = Sg(A)
 +
| Eigenschaft d. GS
 +
|-
 +
| 2)
 +
| B' = Sg(B)
 +
| Eigenschaft d. GS
 +
|-
 +
| 3)
 +
| C' = Sg(C)
 +
| Eigenschaft d. GS
 +
|-
 +
| 4)
 +
| <math>\\ BA^{+}\  \tilde {=}\ \ B'A'^{+}</math>
 +
| (1); (2); Voraussetzung; Halbgeradentreue d. GS
 +
|-
 +
| 5)
 +
| <math>\\ BC^{+}\  \tilde {=}\ \ B'C'^{+}</math>
 +
| (2); (3); Voraussetzung; Halbgeradentreue d. GS
 +
|-
 +
| 6)
 +
| <math>\left| \angle ABC\  \right|\ =\ \left| \angle A'B'C'\  \right| </math>
 +
| (4); (5); Winkelmaßerhaltung d. GS;
 +
|-
 +
| 7)
 +
| <math>\angle ABC\  \tilde {=} \ \angle A'B'C' </math>
 +
| (4); (5); (6); Winkelkongruenz
 +
q.e.d.
 +
|}--[[Benutzer:Nolessonlearned|Nolessonlearned]] 13:27, 15. Jul. 2013 (CEST)<br />

Version vom 15. Juli 2013, 12:27 Uhr

Beweisen Sie die Winkeltreue der Geradenspiegelung. Nutzen Sie für den Beweis die Halbgeradentreue und die Eigenschaft der Geradenspiegelung winkelmaßerhaltend zu sein.


Voraussetzung 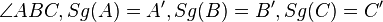\angle ABC, Sg(A)=A', Sg(B)=B', Sg(C)=C'
Behauptung 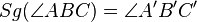Sg(\angle ABC ) = \angle A'B'C'



Beweisschritt Begründung
1 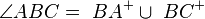\angle ABC = \ BA^{+} \cup \ BC^{+} Voraussetzung, Def. Winkel
2 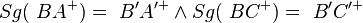Sg(\ BA^{+} ) = \ B'A'^{+} \wedge Sg (\ BC^{+} ) = \ B'C'^{+} Halbgeradentreue, 1)
3 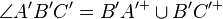\angle A'B'C' = B'A'^{+} \cup B'C'^{+} Def Winkel, 2)
4 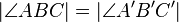|\angle ABC| = |\angle A'B'C'| Winkelmaßerhaltend
5 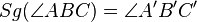Sg(\angle ABC ) = \angle A'B'C' 1)2)4)

--Regenschirm 18:13, 25. Jun. 2013 (CEST)

Der Beweis ist korrekt.--Tutorin Anne 15:16, 26. Jun. 2013 (CEST)





Voraussetzung:
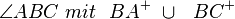
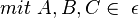
\angle ABC\ mit\ \ BA^{+}\ \cup\ \ BC^{+}\ mit\ A,B,C \in\ \epsilon

Behauptung: 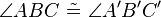\angle ABC\ \tilde {=}\ \angle A'B'C'

Beweisschritt Begründung
1) A' = Sg(A) Eigenschaft d. GS
2) B' = Sg(B) Eigenschaft d. GS
3) C' = Sg(C) Eigenschaft d. GS
4) Fehler beim Parsen(Syntaxfehler): \\ BA^{+}\ \tilde {=}\ \ B'A'^{+} (1); (2); Voraussetzung; Halbgeradentreue d. GS
5) Fehler beim Parsen(Syntaxfehler): \\ BC^{+}\ \tilde {=}\ \ B'C'^{+} (2); (3); Voraussetzung; Halbgeradentreue d. GS
6) 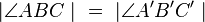\left| \angle ABC\ \right|\ =\ \left| \angle A'B'C'\ \right| (4); (5); Winkelmaßerhaltung d. GS;
7) 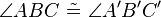\angle ABC\ \tilde {=} \ \angle A'B'C' (4); (5); (6); Winkelkongruenz

q.e.d.

--Nolessonlearned 13:27, 15. Jul. 2013 (CEST)
Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_9.3P_(SoSe_13)&oldid=24686“