Lösung von Aufg. 12.04 SoSe 13: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Lösung)
(→‎Lösung)
Zeile 9: Zeile 9:
 
'''Annahme:'''<br />
 
'''Annahme:'''<br />
 
::<math>t \not \perp \overline{MB}</math>.<br />
 
::<math>t \not \perp \overline{MB}</math>.<br />
−
Nach der Existenz des Lotes von <math>M</math> auf <math>t</math> muss es jetzt eine Strecke <math>\overline{MA}</math> geben, die das Lot von <math>M</math> auf <math>t</math> ist. Selbstverständlich ist <math>A</math> verschieden von <math>B</math>, da ansonsten <math>t \perp \overline{MB}</math>.
+
Nach der Existenz des Lotes von <math>M</math> auf <math>t</math> muss es jetzt eine Strecke <math>\overline{MA}</math> geben, die das Lot von <math>M</math> auf <math>t</math> ist. Selbstverständlich ist <math>A</math> verschieden von <math>B</math>, da ansonsten <math>t \perp \overline{MB}</math> gelten würde. Weil <math>t</math> Tangente an <math>k</math> ist, kann <math>A</math> nit zu <math>k</math> gehören.<br />
 +
 
 +
'''Fall 1:'''<br />
 +
:<math>A</math> liegt außerhalb von <math>k</math>. Der Abstand von <math>A</math> zu <math>M</math> ist nun größer als der Radius <math>|\overline{MB}|</math>. <math>\overline{MB}</math> liegt jedoch in <math>\overline{MAB}</math> dem rechten Winkel gegenüber und muss demzufolge die längst der Seiten von <math>\overline{MAB}</math> sein.<br />
 +
'''Fall 2:'''<br />
 +
: <math>A</math> liegt innerhalb von <math>k</math>.
  
 
Zurück zu: [[Serie 12 SoSe 2013]]
 
Zurück zu: [[Serie 12 SoSe 2013]]

Version vom 18. Juli 2013, 21:23 Uhr

Aufgabe 12.04

Die Gerade t sei Tangente an den Kreis k (Mittelpunkt M) im Punkt B. Beweisen Sie: 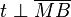t \perp \overline{MB}.

Lösung

Annahme:

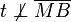t \not \perp \overline{MB}.

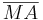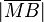Nach der Existenz des Lotes von M auf t muss es jetzt eine Strecke \overline{MA} geben, die das Lot von M auf t ist. Selbstverständlich ist A verschieden von B, da ansonsten t \perp \overline{MB} gelten würde. Weil t Tangente an k ist, kann A nit zu k gehören.

Fall 1:

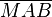A liegt außerhalb von k. Der Abstand von A zu M ist nun größer als der Radius |\overline{MB}|. \overline{MB} liegt jedoch in \overline{MAB} dem rechten Winkel gegenüber und muss demzufolge die längst der Seiten von \overline{MAB} sein.

Fall 2:

A liegt innerhalb von k.

Zurück zu: Serie 12 SoSe 2013

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufg._12.04_SoSe_13&oldid=24910“