Lösung von Aufgabe 12.09 SoSe 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Lösung) |
*m.g.* (Diskussion | Beiträge) (→Lösung) |
||
| Zeile 11: | Zeile 11: | ||
Es sei <math>k</math> ein Kreis mit dem Mittelpunkt <math>M</math>.<br /> | Es sei <math>k</math> ein Kreis mit dem Mittelpunkt <math>M</math>.<br /> | ||
Wenn die Punkte <math>A,S,B</math> drei paarweise verschiedene Punkte von <math>k</math> sind, ist <math>\angle ASB</math> ein Peripheriewinkel von <math>k</math>.<br /> | Wenn die Punkte <math>A,S,B</math> drei paarweise verschiedene Punkte von <math>k</math> sind, ist <math>\angle ASB</math> ein Peripheriewinkel von <math>k</math>.<br /> | ||
| − | Jeder Winkel, der <math>M</math> zum Scheitelpunkt hat und mit <math>k</math> in ein und derselben Ebene | + | Jeder Winkel, der <math>M</math> zum Scheitelpunkt hat und mit <math>k</math> in ein und derselben Ebene liegt, ist ein Zentriwinkel von <math>k</math>. |
Zurück zu: [[Serie 12 SoSe 2013]] | Zurück zu: [[Serie 12 SoSe 2013]] | ||
Aktuelle Version vom 18. Juli 2013, 22:08 Uhr
Aufgabe 12.09Informieren Sie sich, was Peripheriewinkel (Umfangswinkel) und Zentriwinkel (Mittelpunktswinkel) sind und definieren Sie diese Begriffe.
LösungEs sei Zurück zu: Serie 12 SoSe 2013 |
ein Kreis mit dem Mittelpunkt 
.
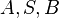drei paarweise verschiedene Punkte von 
ein Peripheriewinkel von 
