Lösung von Aufg. 11.05 SoSe 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) (→Lösung) |
||
| Zeile 8: | Zeile 8: | ||
==Lösung== | ==Lösung== | ||
| − | Es sei <math>\overline{ABC}</math> ein Dreieck mit den schulüblichen Bezeichnungen. Zunächst schneiden sich die Mittelsenkrechten <math>m_c</math> und <math>m_b</math> im Punkt <math>M</math>. (Wären sie parallel, müssten auch <math>AB</math> und <math>BC</math> parallel sein und <math>\overline{ABC}</math> wäre kein Dreieck.) Nach den | + | Es sei <math>\overline{ABC}</math> ein Dreieck mit den schulüblichen Bezeichnungen. Zunächst schneiden sich die Mittelsenkrechten <math>m_c</math> und <math>m_b</math> im Punkt <math>M</math>. (Wären sie parallel, müssten auch <math>AB</math> und <math>BC</math> parallel sein und <math>\overline{ABC}</math> wäre kein Dreieck.) Nach den Eigenschaften von Mittelsenkrechten gilt: <math>|MA|=|MB|</math> und <math>|MB|=|MC|</math>. Nach der Tarnsitivität der Gleicheitsrelation gilt nun: <math>|MA|=|MC|</math>. Nach dem Mittelsenkrechtenkriterium geht jetzt <math>m_b</math> auch durch <math>M</math>.<br /><br />--[[Benutzer:*m.g.*|*m.g.*]] 23:59, 18. Jul. 2013 (CEST)<br /> |
Zurück zu: [[Serie 11 SoSe 2013]] | Zurück zu: [[Serie 11 SoSe 2013]] | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
Version vom 18. Juli 2013, 22:59 Uhr
Aufgabe 10.05Beweisen Sie: Jedes Dreieck hat genau einen Umkreis.
LösungEs sei |
 ein Dreieck mit den schulüblichen Bezeichnungen. Zunächst schneiden sich die Mittelsenkrechten
ein Dreieck mit den schulüblichen Bezeichnungen. Zunächst schneiden sich die Mittelsenkrechten 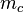 und
und 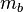 im Punkt
im Punkt  . (Wären sie parallel, müssten auch
. (Wären sie parallel, müssten auch  und
und 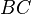 parallel sein und
parallel sein und 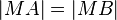 und
und 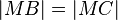 . Nach der Tarnsitivität der Gleicheitsrelation gilt nun:
. Nach der Tarnsitivität der Gleicheitsrelation gilt nun: 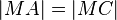 . Nach dem Mittelsenkrechtenkriterium geht jetzt
. Nach dem Mittelsenkrechtenkriterium geht jetzt 
