Lösung von Aufgabe 4.1 P (WS 13/14): Unterschied zwischen den Versionen

Aktuelle Version vom 6. Januar 2014, 15:52 Uhr

Beweisen Sie mit Hilfe einer Wahrheitstabelle:

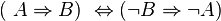
$(\ A \Rightarrow B) \ \Leftrightarrow (\neg B \Rightarrow \neg A)$

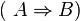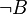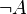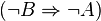
A	B	$(\ A \Rightarrow B) \$	$\neg B$	$\neg A$	$(\neg B \Rightarrow \neg A)$
w	w	w	f	f	w
w	f	f	w	f	f
f	w	w	f	w	w
f	f	w	w	w	w

--EarlHickey (Diskussion) 09:14, 6. Jan. 2014 (CET)

Inwiefern hilft Ihnen diese Äquivalenz, wenn Sie einen geometrischen Satz beweisen wollen?

Beim indirekten Beweis durch Kontraposition.
--EarlHickey (Diskussion) 09:14, 6. Jan. 2014 (CET)

so ist es. Ohne diese Grundlage wäre ein Beweis durch Kontraposition nicht sinnvoll. So ist es z.B. bei der Umkehrung eines Satzes: Der Beweis der Umkehrung lässt noch keine Aussage zum Satz selber machen, da die Aussagen nicht äquivalent sind. --Tutorin Anne (Diskussion) 15:52, 6. Jan. 2014 (CET)

@@ Zeile 22: / Zeile 22: @@
 Beim indirekten Beweis durch Kontraposition.<br />
 --[[Benutzer:EarlHickey|EarlHickey]] ([[Benutzer Diskussion:EarlHickey|Diskussion]]) 09:14, 6. Jan. 2014 (CET)<br />
+* so ist es. Ohne diese Grundlage wäre ein Beweis durch Kontraposition nicht sinnvoll. So ist es z.B. bei der Umkehrung eines Satzes: Der Beweis der Umkehrung lässt noch keine Aussage zum Satz selber machen, da die Aussagen nicht äquivalent sind. --[[Benutzer:Tutorin Anne|Tutorin Anne]] ([[Benutzer Diskussion:Tutorin Anne|Diskussion]]) 15:52, 6. Jan. 2014 (CET)
 [[Category:Einführung_P]]