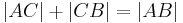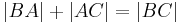Lösung von Zusatzaufgabe 6.2P (WS 13/14): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „Beweisen Sie: Es sei <math> \operatorname{koll} \left( A, B, C \right) </math> mit <math>\ A, B, C</math> sind paarweise verschieden.<br /> Dann gilt genau eine d…“)
 
Zeile 1: Zeile 1:
−
Beweisen Sie: Es sei <math> \operatorname{koll} \left( A, B, C \right) </math> mit <math>\ A, B, C</math> sind paarweise verschieden.<br /> Dann gilt genau eine der folgenden Zwischenrelationen: <math> \operatorname{Zw} \left( A, B, C \right) </math> oder <math> \operatorname{Zw} \left( A, C, B \right) </math> oder <math> \operatorname{Zw} \left( B, A, C \right) </math>.
+
Beweisen Sie: Es sei <math> \operatorname{koll} \left( A, B, C \right) </math> mit <math>\ A, B, C</math> sind paarweise verschieden.<br /> Dann gilt genau eine der folgenden Zwischenrelationen: <math> \operatorname{Zw} \left( A, B, C \right) </math> oder <math> \operatorname{Zw} \left( A, C, B \right) </math> oder <math> \operatorname{Zw} \left( B, A, C \right) </math>.<br>
 +
<br>
 +
Aus der Dreiecksungleichung
 +
::"Für drei beliebige Punkte <math>\ A, B</math> und <math>\ C</math> gilt: <math>\left|AB \right|+ \left| BC \right| \geq \left| AC \right|.</math>
 +
 
 +
::Falls <math>\operatorname{koll} \left( ABC \right)</math>, dann ist eine der folgenden Gleichungen erfüllt:
 +
 
 +
::::<math>\left| AB \right| + \left| BC \right| = \left| AC \right| </math>
 +
::::<math>\left| AC \right| + \left| CB \right| = \left| AB \right| </math>
 +
::::<math>\left| BA \right| + \left| AC \right| = \left| BC \right| </math><br />
 +
::Ist umgekehrt eine dieser drei Gleichungen erfüllt, so sind <math>\ A</math>, <math>\ B</math> und <math>\ C</math> kollinear."<br>
 +
folgt unmittelbar unter Verwendung von der Definition I.2: (Zwischenrelation)
 +
::::"Ein Punkt <math>\ B</math> liegt zwischen zwei Punkten <math>\ A</math> und <math>\ C</math>, wenn <math> \left| AB \right| + \left| BC \right| = \left| AC \right| </math> gilt und der Punkt <math>\ B</math> sowohl von <math>\ A</math> als auch von <math>\ C</math> verschieden ist.
 +
 
 +
::::Schreibweise: <math> \operatorname{Zw} \left( A, B, C \right) </math>"<br>
 +
die Behauptung.<br>
 +
<br>
 +
--[[Benutzer:EarlHickey|EarlHickey]] ([[Benutzer Diskussion:EarlHickey|Diskussion]]) 13:19, 4. Feb. 2014 (CET)
 +
 
  
  
  
 
[[Kategorie:Einführung_P]]
 
[[Kategorie:Einführung_P]]

Version vom 4. Februar 2014, 13:19 Uhr

Beweisen Sie: Es sei \operatorname{koll} \left( A, B, C \right) mit \ A, B, C sind paarweise verschieden.
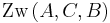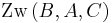Dann gilt genau eine der folgenden Zwischenrelationen: \operatorname{Zw} \left( A, B, C \right) oder \operatorname{Zw} \left( A, C, B \right) oder \operatorname{Zw} \left( B, A, C \right) .

Aus der Dreiecksungleichung

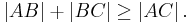
"Für drei beliebige Punkte \ A, B und \ C gilt: \left|AB \right|+ \left| BC \right| \geq \left| AC \right|.
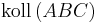Falls \operatorname{koll} \left( ABC \right), dann ist eine der folgenden Gleichungen erfüllt:
\left| AB \right| + \left| BC \right| = \left| AC \right|
\left| AC \right| + \left| CB \right| = \left| AB \right|
\left| BA \right| + \left| AC \right| = \left| BC \right|
Ist umgekehrt eine dieser drei Gleichungen erfüllt, so sind \ A, \ B und \ C kollinear."

folgt unmittelbar unter Verwendung von der Definition I.2: (Zwischenrelation)

"Ein Punkt \ B liegt zwischen zwei Punkten \ A und \ C, wenn \left| AB \right| + \left| BC \right| = \left| AC \right| gilt und der Punkt \ B sowohl von \ A als auch von \ C verschieden ist.
Schreibweise: \operatorname{Zw} \left( A, B, C \right) "

die Behauptung.

--EarlHickey (Diskussion) 13:19, 4. Feb. 2014 (CET)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Zusatzaufgabe_6.2P_(WS_13/14)&oldid=25858“