Vorlage:Lösungen: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „{| border="0" cellpadding="5" cellspacing="2" style="border-left: 10px solid {{{RandLinks|#8E8CF2}}}; margin-bottom: 0.4em; margin-left: auto; margin-right: auto;...“) |
K (1 Version: Aktualisierung) |
||
| (3 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | =Aufgabe 7.1= | |
| − | + | Es seien <math>a, b</math> und <math>c</math> drei zueinander parallele Geraden (paarweise nicht identisch). Man konstruiere ein gleichseitiges Dreieck <math>\overline{ABC}</math> derart, dass <math>A \in a, B \in b, C \in c</math> gilt. | |
| − | + | ||
| − | </ | + | |
| − | + | ||
| − | + | ||
| − | { | + | [[Vorlage: Lösung 7.1]] |
| − | < | + | |
| − | </ | + | =Aufgabe 7.2= |
| − | < | + | Es seien <math>k_1, k_2, k_3</math> drei konzentrische Kreise mit den Radien <math>r_1, r_2, r_3</math>. Es gelte <math>0<r_1<r_2<r_3</math>. Man konstruiere ein gleichseitiges Dreieck <math>\overline{ABC}</math> derart, dass <math>A \in k_1, B \in k_2, C \in k_3</math> gilt. |
| + | =Aufgabe 7.3= | ||
| + | Es sei <math>\overline{ABC}</math> ein gleichseitiges Dreieck. <math>s_a</math> sei der dem Winkel <math>\angle BAC</math> zugehörige Kreisbogen auf dem Kreis um <math>A</math> durch <math>B</math>. Analog sind die Kreisbögen <math>s_b</math> und <math>s_c</math> zu verstehen. Unter dem Reuleaux-Dreieck <math>\widetilde{ABC}</math> versteht man die Vereinigungsmenge <math>s_a \cup s_b \cup s_c</math>. | ||
| + | Man berechne den Umfang von <math>\widetilde{ABC}</math> in Abhängigkeit von <math>|AB|</math>. | ||
| + | [[Kategorie:Elementargeometrie]] | ||
Aktuelle Version vom 8. Februar 2014, 22:16 Uhr
Aufgabe 7.1
Es seien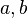 
und 
drei zueinander parallele Geraden (paarweise nicht identisch). Man konstruiere ein gleichseitiges Dreieck 
derart, dass 
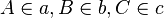gilt.
Aufgabe 7.2
Es seien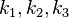 
drei konzentrische Kreise mit den Radien 
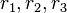. Es gelte 
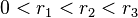. Man konstruiere ein gleichseitiges Dreieck derart, dass 
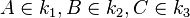gilt.
Aufgabe 7.3
Es sei ein gleichseitiges Dreieck.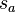 
sei der dem Winkel 
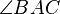zugehörige Kreisbogen auf dem Kreis um 
durch 
. Analog sind die Kreisbögen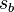 
und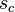 
zu verstehen. Unter dem Reuleaux-Dreieck 
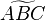versteht man die Vereinigungsmenge 
.
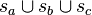Man berechne den Umfang von 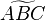in Abhängigkeit von 
.
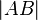