Lösung von Aufgabe 12.5P (WS 13/14): Unterschied zwischen den Versionen

Version vom 10. Februar 2014, 10:21 Uhr

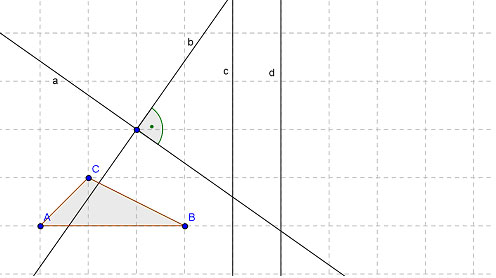
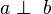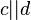Gegeben sei ein Dreieck $\overline{ABC}$ und die Geraden a, b, c und d mit: $\ a \perp \ b$ und $c||d$ entsprechend der Skizze.

Durch welche Abbildung kann die Verkettung der vier Geradenspiegelungen 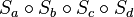$S_{a}\circ S_{b}\circ S_{c}\circ S_{d}$ ersetzt werden (Begründen Sie Ihre Entscheidung)?
Zeichnen Sie die Achsen der Ersatzabbildung in die Skizze oben ein. Hinweis: Sie dürfen das Gitter im Hintergrund als Orientierung nutzen.
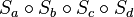Konstruieren Sie oben in der Skizze das Bild des Dreiecks $\overline{ABC}$ , das nach der Verkettung $S_{a}\circ S_{b}\circ S_{c}\circ S_{d}$ entsteht, mit Hilfe der Ersatzabbildung.

Lösung:
1.)

(1) Drehe $a$ und $b$ gleichsinnig um den gleichen Winkel um ihren Schnittpunkt $S$ , bis $b$ parallel zu $c$ ist. | "Eig. der Drehung"

Man erhät 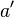$a'$ und $b'$ .

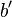(2) Verschiebe $c$ und $d$ gleichsinnig und mit dem gleichen Betrag, solange bis $c$ auf $b$ zu liegen kommt. | "Eig. der Geradenspiegelung

Man erhät 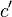$c'$ und $d'$ .

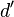(3) Die Geradenspiegelung an $b$ und $c$ heben sich auf (sind involutorisch). | "Eig. der Geradenspiegelung"

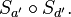
(4) Die Abbildung reduziert sich auf $S_{a'} \circ S_{d'}.$

--EarlHickey (Diskussion) 09:46, 10. Feb. 2014 (CET)

@@ Zeile 4: / Zeile 4: @@
 <br /><br />
 #Durch welche Abbildung kann die Verkettung der vier Geradenspiegelungen <math>S_{a}\circ S_{b}\circ S_{c}\circ S_{d} </math> ersetzt werden (Begründen Sie Ihre Entscheidung)?
+#Zeichnen Sie die Achsen der Ersatzabbildung in die Skizze oben ein. Hinweis: Sie dürfen das Gitter im Hintergrund als Orientierung nutzen.
+#Konstruieren Sie oben in der Skizze das Bild des Dreiecks <math>\overline{ABC}</math>, das nach der Verkettung <math>S_{a}\circ S_{b}\circ S_{c}\circ S_{d} </math> entsteht, mit Hilfe der Ersatzabbildung.<br />
+Lösung:<br>
+.)<Br>
 ::(1) Drehe <math> a </math> und <math> b </math> gleichsinnig um den gleichen Winkel um ihren Schnittpunkt <math> S</math>, bis <math> b </math> parallel zu <math> c </math> ist. | "Eig. der Drehung"<br>
 ::Man erhät <math> a' </math> und <math> b' </math>.<br>
@@ Zeile 11: / Zeile 16: @@
 ::(4) Die Abbildung reduziert sich auf <math> S_{a'} \circ S_{d'}.</math><br>
 ::--[[Benutzer:EarlHickey|EarlHickey]] ([[Benutzer Diskussion:EarlHickey|Diskussion]]) 09:46, 10. Feb. 2014 (CET)<br>
-#Zeichnen Sie die Achsen der Ersatzabbildung in die Skizze oben ein. Hinweis: Sie dürfen das Gitter im Hintergrund als Orientierung nutzen.
-#Konstruieren Sie oben in der Skizze das Bild des Dreiecks <math>\overline{ABC}</math>, das nach der Verkettung <math>S_{a}\circ S_{b}\circ S_{c}\circ S_{d} </math> entsteht, mit Hilfe der Ersatzabbildung.<br />
 [[Kategorie:Einführung_P]]