Lösung von Zusatzaufgabe 12.2P (WS 13/14): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Zeigen Sie, dass die Verkettung einer Drehung <math>D_{\left( S,\alpha \right) } </math> mit einer Verschiebung wieder eine Drehung <math>D_{\left( P,\alpha \r…“) |
|||
| Zeile 1: | Zeile 1: | ||
Zeigen Sie, dass die Verkettung einer Drehung <math>D_{\left( S,\alpha \right) } </math> mit einer Verschiebung wieder eine Drehung <math>D_{\left( P,\alpha \right) } </math> ergibt. Wo liegt das neue Drehzentrum ''P''? | Zeigen Sie, dass die Verkettung einer Drehung <math>D_{\left( S,\alpha \right) } </math> mit einer Verschiebung wieder eine Drehung <math>D_{\left( P,\alpha \right) } </math> ergibt. Wo liegt das neue Drehzentrum ''P''? | ||
<br /> | <br /> | ||
| + | ::(1) <math> D_{(S,\alpha)}:= S_a\circ S_b </math><br> | ||
| + | ::(2) Verschiebung <math>T := S_c\circ S_d </math><br> | ||
| + | ::(3) Es sei <math>S_{alt}\in a,b </math><br> | ||
| + | ::(4) Drehe <math> a </math> und <math>b </math> so um <math> D_{alt} </math>, dass <math> b'||c </math> gilt. Es entsteht <math> a' </math> und <math> b' </math><br> | ||
| + | ::(5) Verschiebe <math> c </math> und <math> d </math> so, dass <math> c </math> auf <math> b' </math> fällt. Es entsteht <math> c'=b' </math> und <math> d' </math>.<br> | ||
| + | ::(6) <math> b' </math> und <math> c' </math> heben sich auf (involutorisch!).<br> | ||
| + | ::(7) Der Punkt <math> S_{neu} \in a',d' </math> ist der neue Drehpunkt der resultierenden Drehung.<br> | ||
| + | ::--[[Benutzer:EarlHickey|EarlHickey]] ([[Benutzer Diskussion:EarlHickey|Diskussion]]) 11:25, 10. Feb. 2014 (CET) | ||
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
Version vom 10. Februar 2014, 11:25 Uhr
Zeigen Sie, dass die Verkettung einer Drehung 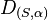 mit einer Verschiebung wieder eine Drehung
mit einer Verschiebung wieder eine Drehung 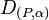 ergibt. Wo liegt das neue Drehzentrum P?
ergibt. Wo liegt das neue Drehzentrum P?
- (1)
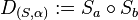
- (2) Verschiebung
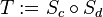
- (3) Es sei
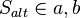
- (4) Drehe
 und
und  so um
so um 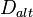 , dass
, dass 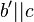 gilt. Es entsteht
gilt. Es entsteht 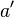 und
und 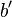
- (5) Verschiebe
 und
und  so, dass
so, dass  auf
auf 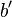 fällt. Es entsteht
fällt. Es entsteht 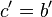 und
und 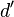 .
.
- (6)
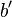 und
und 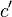 heben sich auf (involutorisch!).
heben sich auf (involutorisch!).
- (7) Der Punkt
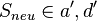 ist der neue Drehpunkt der resultierenden Drehung.
ist der neue Drehpunkt der resultierenden Drehung.
- --EarlHickey (Diskussion) 11:25, 10. Feb. 2014 (CET)
- (1)

