Übung 27.10.14: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 1: | Zeile 1: | ||
| − | Es sei p = , F = (0, p | + | Es sei p = <math>\frac{1}{2}</math>, F = (0, <math>\frac{p}{2}</math>). |
| − | Die Gerade l sei durch die Gleichung y = -p | + | Die Gerade l sei durch die Gleichung y = - <math>\frac{p}{2}</math> gegeben. |
| − | L = (x, -p | + | L = (x, - <math>\frac{p}{2}</math>) sei ein beliebiger Punkt auf l. |
| − | Der Punkt P sei der Schnittpunkt der Mittelsenkrechten m von LF mit der in L auf l errichteten Senkrechten s. | + | Der Punkt P sei der Schnittpunkt der Mittelsenkrechten m von <span style="border-top:1px solid">LF</span> mit der in L auf l errichteten Senkrechten s. |
| − | 1. Man überlege: Wieso gilt: FP = Pl? | + | 1. Man überlege: Wieso gilt: <span style="border-top:1px solid">FP</span> = <span style="border-top:1px solid">Pl</span>? |
2. Man beweise: m ist Tangente an die Normalparabel y(x) = x<sup>2</sup> in P. | 2. Man beweise: m ist Tangente an die Normalparabel y(x) = x<sup>2</sup> in P. | ||
Aktuelle Version vom 3. Dezember 2014, 16:35 Uhr
Es sei p =  , F = (0,
, F = (0, 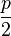 ).
).
Die Gerade l sei durch die Gleichung y = - 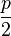 gegeben.
gegeben.
L = (x, - 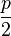 ) sei ein beliebiger Punkt auf l.
) sei ein beliebiger Punkt auf l.
Der Punkt P sei der Schnittpunkt der Mittelsenkrechten m von LF mit der in L auf l errichteten Senkrechten s.
1. Man überlege: Wieso gilt: FP = Pl?
2. Man beweise: m ist Tangente an die Normalparabel y(x) = x2 in P.

