Übung 08.12.14: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „= Aufgabe III.01 = Gegeben seien die Gerade <math>l</math> durch die Geradengleichung <math>y(x)=-\frac{1}{4}</math> und der Punkt <math>F \left(0,\frac{1}{4} …“) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe III.01) |
||
| Zeile 1: | Zeile 1: | ||
= Aufgabe III.01 = | = Aufgabe III.01 = | ||
| − | Gegeben seien die Gerade <math>l</math> durch die Geradengleichung <math>y(x)=-\frac{1}{4}</math> und der Punkt <math>F \left(0,\frac{1}{4} \right)</math>. | + | Gegeben seien die Gerade <math>l</math> durch die Geradengleichung <math>y(x)=-\frac{1}{4}</math> und der Punkt <math>F \left(0,\frac{1}{4} \right)</math>. Beweisen Sie: Für jeden beliebigen Punkt <math>L</math> auf <math>l</math> gilt: Der Schnittpunkt der Senkrechten <math>s</math> auf <math>l</math> in <math>L</math> mit der Mittelsenkrechten von <math>\overline{FL}</math> ist ein Punkt der Normalparabel. |
Version vom 4. Dezember 2014, 17:03 Uhr
Aufgabe III.01
Gegeben seien die Gerade  durch die Geradengleichung
durch die Geradengleichung 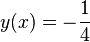 und der Punkt
und der Punkt 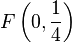 . Beweisen Sie: Für jeden beliebigen Punkt
. Beweisen Sie: Für jeden beliebigen Punkt  auf
auf  gilt: Der Schnittpunkt der Senkrechten
gilt: Der Schnittpunkt der Senkrechten  auf
auf  in
in  mit der Mittelsenkrechten von
mit der Mittelsenkrechten von 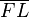 ist ein Punkt der Normalparabel.
ist ein Punkt der Normalparabel.

