Übung 08.12.14: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Aufgabe III.01) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe III.02) |
||
| Zeile 5: | Zeile 5: | ||
= Aufgabe III.02 = | = Aufgabe III.02 = | ||
| + | In der Mathematikdidaktik spricht man gern vom ''Spiralprinzip'' der Vermittlung mathematischen Lehrstoffs. Warum wäre der Begriff ''Schraubenlinienprinzip'' angebrachter? | ||
Version vom 4. Dezember 2014, 17:14 Uhr
Aufgabe III.01
Gegeben seien die Gerade 
durch die Geradengleichung 
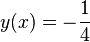und der Punkt 
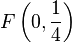. Beweisen Sie: Für jeden beliebigen Punkt 
auf gilt: Der Schnittpunkt 
der Senkrechten 
auf in mit der Mittelsenkrechten von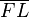 
ist ein Punkt der Normalparabel.
Aufgabe III.02
In der Mathematikdidaktik spricht man gern vom Spiralprinzip der Vermittlung mathematischen Lehrstoffs. Warum wäre der Begriff Schraubenlinienprinzip angebrachter?
