Lösung von Aufgabe 1.1 (WS 16 17): Unterschied zwischen den Versionen

Aus Geometrie-Wiki

Wechseln zu: Navigation, Suche

@@ Zeile 1: / Zeile 1: @@
 Es sei A die Menge der geraden natürlichen Zahlen, B die Menge der natürlichen Zahlen, deren Quadrate gerade ist. Vergleichen Sie die Mengen.<br />
+<popup>
+Kurz gesagt <math>A = B</math>.
+==Beweis==
+Zu beweisen ist, dass gilt: <math>x \text{ ist gerade} \iff x^2 \text{ ist gerade}</math>
+===Teil 1===
+Gezeigt wird <math>x \text{ ist gerade} \Rightarrow x^2 \text{ ist gerade}</math>.
+Zunächst nehmen wir an, dass <math>x = 2 \cdot n \text{für} n \in \mathbb{N}</math>.
+Das heißt, dass <math>x^2 = (2n)\cdot(2n) = 2\cdot(2n^2)</math> gilt. Und da <math>2n^2 \in \mathbb{N}</math>, ist <math>x^2</math> ein ganzzahliges Vielfaches von <math>2</math> oder anders ausgedrückt gerade.
+===Teil 2===
+Gezeigt wird <math>x \text{ ist gerade} \Leftarrow x^2 \text{ ist gerade}</math>.
+Sei nun <math>x^2 = 2 \cdot n</math> für <math>x, n \in \mathbb{N}</math>.
+Damit gilt: <math>\frac{x \cdot x}{2} = n \iff x \cdot \frac{x}{2} = n</math>.
+Da sowohl <math>x</math> als auch <math>n</math> natürliche Zahlen sind, kann die Gleichung nur wahr sein, wenn <math>\frac{x}{2}</math> auch eine natürliche Zahl ist. <math>\frac{x}{2}</math> wiederum kann nur eine natürliche Zahl sein, wenn <math>x</math> gerade ist.
+q.e.d.
+</popup>--[[Benutzer:AlanTu|AlanTu]] ([[Benutzer Diskussion:AlanTu|Diskussion]]) 22:55, 20. Okt. 2016 (CEST)
 [[Kategorie:Geo_P]]
+[[Kategorie:Lösung zu Übung 1 (Wintersemester 2016/2017)]]

Version vom 20. Oktober 2016, 21:55 Uhr

Es sei A die Menge der geraden natürlichen Zahlen, B die Menge der natürlichen Zahlen, deren Quadrate gerade ist. Vergleichen Sie die Mengen.

anzeigen

verstecken

Kurz gesagt $A = B$ .

Beweis

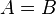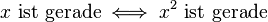
Zu beweisen ist, dass gilt: $x \text{ ist gerade} \iff x^2 \text{ ist gerade}$

Teil 1

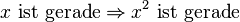Gezeigt wird $x \text{ ist gerade} \Rightarrow x^2 \text{ ist gerade}$ .

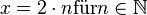Zunächst nehmen wir an, dass $x = 2 \cdot n \text{für} n \in \mathbb{N}$ .

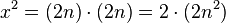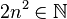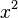Das heißt, dass $x^2 = (2n)\cdot(2n) = 2\cdot(2n^2)$ gilt. Und da $2n^2 \in \mathbb{N}$ , ist $x^2$ ein ganzzahliges Vielfaches von 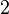$2$ oder anders ausgedrückt gerade.

Teil 2

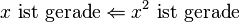Gezeigt wird $x \text{ ist gerade} \Leftarrow x^2 \text{ ist gerade}$ .

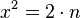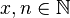Sei nun $x^2 = 2 \cdot n$ für $x, n \in \mathbb{N}$ .

Damit gilt: $\frac{x \cdot x}{2} = n \iff x \cdot \frac{x}{2} = n$ .

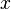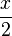Da sowohl $x$ als auch $n$ natürliche Zahlen sind, kann die Gleichung nur wahr sein, wenn $\frac{x}{2}$ auch eine natürliche Zahl ist. $\frac{x}{2}$ wiederum kann nur eine natürliche Zahl sein, wenn $x$ gerade ist.