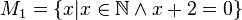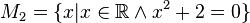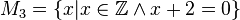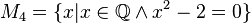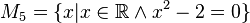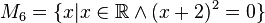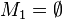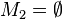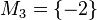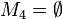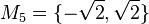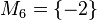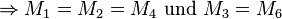Lösung von Aufgabe 1.2 (WS 16 17): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „Geben Sie eine andere Schreibweise der folgenden Mengen an und prüfen Sie, welche Mengen identisch sind.<br /><br /> <math>M_1 = \{x\vert x\in \mathbb{N}\wedg…“)
 
(Meine Lösung hinzugefügt.)
Zeile 7: Zeile 7:
 
<math>M_6 = \{x\vert x\in \mathbb{R}\wedge (x+2)^{2} = 0\}</math><br /><br />
 
<math>M_6 = \{x\vert x\in \mathbb{R}\wedge (x+2)^{2} = 0\}</math><br /><br />
  
 +
<popup>
 +
<math>M_1 = \emptyset</math>
  
 +
<math>M_2 = \emptyset</math>
 +
 +
<math>M_3 = \{-2\}</math>
 +
 +
<math>M_4 = \emptyset</math>
 +
 +
<math>M_5 = \{-\sqrt{2}, \sqrt{2}\}</math>
 +
 +
<math>M_6 = \{-2\}</math>
 +
 +
<math>\Rightarrow M_1 = M_2 = M_4 \text{ und } M_3 = M_6</math>
 +
</popup>--[[Benutzer:AlanTu|AlanTu]] ([[Benutzer Diskussion:AlanTu|Diskussion]]) 23:53, 20. Okt. 2016 (CEST)
  
  
  
 
[[Kategorie:Geo_P]]
 
[[Kategorie:Geo_P]]
 +
[[Kategorie:Lösung zu Übung 1 (Wintersemester 2016/2017)]]

Version vom 20. Oktober 2016, 22:53 Uhr

Geben Sie eine andere Schreibweise der folgenden Mengen an und prüfen Sie, welche Mengen identisch sind.

M_1 = \{x\vert x\in \mathbb{N}\wedge x+2 = 0\}

M_2 = \{x\vert x\in \mathbb{R}\wedge x^{2}+2 = 0\}

M_3 = \{x\vert x\in \mathbb{Z}\wedge x+2 = 0\}

M_4 = \{x\vert x\in \mathbb{Q}\wedge x^{2}-2 = 0\}

M_5 = \{x\vert x\in \mathbb{R}\wedge x^{2}-2 = 0\}

M_6 = \{x\vert x\in \mathbb{R}\wedge (x+2)^{2} = 0\}

--AlanTu (Diskussion) 23:53, 20. Okt. 2016 (CEST)
Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_1.2_(WS_16_17)&oldid=28439“