Benutzer:Regenbogen: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
Zeile 18: Zeile 18:
 
Volumen V:
 
Volumen V:
 
<math>V = G \ast h = \pi \ast r^2 \ast h</math>
 
<math>V = G \ast h = \pi \ast r^2 \ast h</math>
 +
 +
Hallo Regenbogen,
 +
eine originelle Verpackung hast du da ;)<br />
 +
Eine kleine Anmerkung:
 +
Du hast ''den Umfang'' als Formel mitaufgelistet, jedoch kann man diesen nur von geometrischen Figuren (2 dimensional)
 +
berechnen und nicht von geometrischen Körpern (3 dimensional), wie einem Zylinder etwa.
 +
Wäre toll, wenn du noch einige Maße angeben kannst, damit man alle genannten Formeln anwenden kann. <br />
 +
Gruß Alex --[[Benutzer:Tutor: Alex|Tutor: Alex]] ([[Benutzer Diskussion:Tutor: Alex|Diskussion]]) 19:18, 27. Okt. 2016 (CEST)

Version vom 27. Oktober 2016, 18:18 Uhr

Studentin, B.A. Lehramtsbezug Sonderpädagogik, Blindenpädagogik, Gehörlosenpädagogik, Mathe, Deutsch

Bild der Verpackung eines Lautsprechers.

Man sieht die zylinderförmige Verpackung eines Lautsprechers.

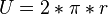
Umfang U: U = 2 \ast \pi \ast r

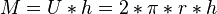
Mantelfläche M: M = U \ast h = 2 \ast \pi \ast r \ast h

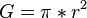
Grundfläche G: G = \pi \ast r^2

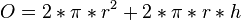
Oberfläche O: O = 2 \ast \pi \ast r^2 + 2 \ast \pi \ast r \ast h

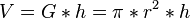
Volumen V: V = G \ast h = \pi \ast r^2 \ast h 

Hallo Regenbogen,
eine originelle Verpackung hast du da ;)

Eine kleine Anmerkung: 
Du hast den Umfang als Formel mitaufgelistet, jedoch kann man diesen nur von geometrischen Figuren (2 dimensional) 
berechnen und nicht von geometrischen Körpern (3 dimensional), wie einem Zylinder etwa. 
Wäre toll, wenn du noch einige Maße angeben kannst, damit man alle genannten Formeln anwenden kann. 

Gruß Alex --Tutor: Alex (Diskussion) 19:18, 27. Okt. 2016 (CEST)
Von „http://geometrie.zum.de/index.php?title=Benutzer:Regenbogen&oldid=28695“