Lösung von Aufgabe 2.2 (WS 16/17): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
K (Verwende Vorlage für Aufgabentext)
(Meine Lösung hinzugefügt.)
Zeile 1: Zeile 1:
 
{{WS2016-2017/MAT01/Mathematische Grundlagen Ⅱ: Geometrie/Woche 2/Aufgabe 2}}
 
{{WS2016-2017/MAT01/Mathematische Grundlagen Ⅱ: Geometrie/Woche 2/Aufgabe 2}}
  
−
[[Kategorie:Geo_P]]
+
<popup name="Lösung von AlanTu">
 +
===Viereck===
 +
Ein Viereck ist ein '''n-Eck''' mit <math>n=4</math>.
 +
 
 +
===Trapez===
 +
Ein Trapez ist ein '''Viereck''' mit zwei zueinander parallelen Seiten.
 +
 
 +
===Gleichschenkliges Trapez===
 +
Ein gleichschenkliges Trapez ist ein '''Trapez''', bei dem die Mittelsenkrechten der beiden parallelen Seiten identisch sind.
 +
 
 +
===Parallelogramm===
 +
Ein Parallelogramm ist ein '''Trapez''', das zwei Paare paralleler Seiten besitzt.
 +
 
 +
===Drachen===
 +
Ein Drachen ist ein '''schiefer Drachen''', bei dem eine Diagonale gleichzeitig Symmetrieachse des Drachen ist.
 +
 
 +
===Schiefer Drachen===
 +
Ein schiefer Drachen ist ein '''Viereck''', bei dem mindestens eine der beiden Diagonale die jeweils andere Diagonale halbiert.
 +
 
 +
===Raute===
 +
Eine Raute ist ein '''Drachen''' mit vier gleich langen Seiten.
 +
 
 +
===Rechteck===
 +
Ein Rechteck ist sowohl ein '''Parallelogramm''' als auch ein '''gleichschenkliges Trapez'''.
 +
 
 +
===Quadrat===
 +
Ein Quadrat ist sowohl eine '''Raute''' als auch ein '''Rechteck'''.
 +
 
 +
</popup>--[[Benutzer:AlanTu|AlanTu]] ([[Benutzer Diskussion:AlanTu|Diskussion]]) 20:05, 2. Nov. 2016 (CET)
 +
 
 +
[[Kategorie:Geo P]]
 
[[Kategorie:Lösung zu Übung 2 (Wintersemester 2016/2017)]]
 
[[Kategorie:Lösung zu Übung 2 (Wintersemester 2016/2017)]]

Version vom 2. November 2016, 20:05 Uhr

Definieren Sie die folgenden Begriffe mathematisch korrekt. Die Begriffe n-Eck, Seite und Ecke eines n-Ecks seien bereits definiert. Beziehen Sie sich auf den nächsthöheren Oberbegriff.

Viereck, Trapez, gleichschenkliges Trapez, Parallelogramm, Drachen, Schiefer Drachen, Raute, Rechteck, Quadrat

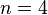--AlanTu (Diskussion) 20:05, 2. Nov. 2016 (CET)
Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_2.2_(WS_16/17)&oldid=28728“