Lösung von Aufgabe 2.2 (WS 16/17): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 60: | Zeile 60: | ||
Draus ergeben sich, durch die anderen Eigenschaften, dass jeder Winkel 90° ist. <br /> | Draus ergeben sich, durch die anderen Eigenschaften, dass jeder Winkel 90° ist. <br /> | ||
Mach weiter so! Top ;) <br /> | Mach weiter so! Top ;) <br /> | ||
| − | Gruß Alex --[[Benutzer:Tutor: Alex|Tutor: Alex]] ([[Benutzer Diskussion:Tutor: Alex|Diskussion]]) | + | Nachtrag: Winkel haben wir ja noch gar nicht definiert ;( Also müssen wir diese Definitionen erstmal außer Acht lassen. <br /> |
| + | Gruß Alex--[[Benutzer:Tutor: Alex|Tutor: Alex]] ([[Benutzer Diskussion:Tutor: Alex|Diskussion]]) 09:37, 3. Nov. 2016 (CET) | ||
Version vom 3. November 2016, 09:37 Uhr
Definieren Sie die folgenden Begriffe mathematisch korrekt. Die Begriffe n-Eck, Seite und Ecke eines n-Ecks seien bereits definiert. Beziehen Sie sich auf den nächsthöheren Oberbegriff.
Viereck, Trapez, gleichschenkliges Trapez, Parallelogramm, Drachen, Schiefer Drachen, Raute, Rechteck, Quadrat
Hallo AlanTu, hier ein paar Anmerkungen zu deiner Lösung:
Bei der Definition des Gleichschenkligen Trapez kannst du auch einfach sagen, dass es eine Symmetrieachse besitzt, die nicht auf einer der Diagonalen liegt (somit Mittelsenkrechte der beiden parallelen Seiten).
Bei dem Parallelogramm hast du schon impliziert, durch das Trapez, dass dieses Viereck schon ein paar parallele Seiten besitzt, sprich, ergänze einfach nur noch um ein Paar und schreibe nicht nochmal zwei Paare paralleler Seiten.
Eine Ergänzung zum Drachen: Deine Definition ist richtig, man kann aber auch sagen, dass bei einem Drachen die Diagonalen senkrecht aufeinander stehen.
Zu den letzten drei Definitionen: Geometrische Figuren definiert man, auch in der Schule, durch ihre Eigenschaften. Du hast zwar recht, dass bspw. ein Quadrat sowohl eine Raute, als auch ein Rechteck ist, aber wäre es nicht schöner zu sagen, es handelt sich um eine Raute mit einem rechten Winkel? ;) Ergänzung zum Rechteck: Es genügt zu sagen, dass ein Rechteck ein Parallelogramm ist mit einem rechten Winkel (Minimalanforderung). Draus ergeben sich, durch die anderen Eigenschaften, dass jeder Winkel 90° ist.
Mach weiter so! Top ;)
Nachtrag: Winkel haben wir ja noch gar nicht definiert ;( Also müssen wir diese Definitionen erstmal außer Acht lassen.
Gruß Alex--Tutor: Alex (Diskussion) 09:37, 3. Nov. 2016 (CET)
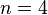 .
.

