Lösung von Aufgabe 13.3P (WS 16/17): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Das Dreieck <math>\overline{ABC}</math> wird an Punkt ''D'' um 90 gedreht. Das gedrehte Dreieck wird nun um den eingezeichneten Vektor verschoben. Gibt es eine…“) |
AlanTu (Diskussion | Beiträge) (Meine Lösung hinzugefügt.) |
||
| Zeile 2: | Zeile 2: | ||
Falls nichts angezeigt wird, können Sie mit folgendem Link [{{fullurl:{{PAGENAME}}|action=purge}} den Servercache leeren].<br /><br /><ggb_applet width="624" height="445" version="4.0" ggbBase64="UEsDBBQACAAIACNe4UAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIACNe4UAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vrdcts2Fr5OnwLDi150IgogSFDMSulEajqbmbTJrLOdnd5BJCyhpgiWpGS504faZ9gn2wOApEhZ/o2tKPFYBkEc4uB855/W+MftKkUbUZRSZROHuNhBIotVIrPFxFlX54OR8+Pr78YLoRZiXnB0rooVryaOryllMnGimMbzkUgG0ZzhgY+pGMwpXDEcJOdRiMMIhw5C21K+ytSvfCXKnMfiLF6KFX+vYl4Zxsuqyl8Nh5eXl27DylXFYrhYzN1tmTgIjpmVE6e+eAXb9R66pIbcw5gM//PLe7v9QGZlxbNYOEiLsJavv3sxvpRZoi7RpUyq5cRh1HPQUsjFEmQK9EmHmigHQHIRV3IjSni0MzUyV6vcMWQ80+sv7BVKW3EclMiNTEQxcbBLCfODgEXMw14AE2CiCimyqiYmNdNhs914I8Wl3VdfGZa+gyql0jnXW6K//0awGUYv9UDs4MHAmF3C9h6mdvDs4NshsDS+fdy3pL6l8S2NTx20kaWcp2LinPO0BAhldl6A+tp5WV2lwpynvrETn7wEmUr5FxBTDHZiMYf7GL/UHwYfXy8M+0KSDteqWD+QacOSef79WXo3s7TTWzjShqPXFZIxED+gL73gBiHZLdjeybOVkgQdnsDK/JrPNY7UewBHO/88hsw/iojjYeMo49o3ULnUtLUiK7EqtbfQCAWRNnqCAvAMFoKNB4hEMIQeAl9AJEB+AFMyQkyPIaIhLPiIohHSdIQi4xrBCP74odmMoQA203dD8EhEgJGPAoqI8SgfgR8h45XgoR4FiiBAATyk2RNPb0EZ8hnM6Aj5cEbtkCEBQgoPwhzYe4gSRPXDJEQeQ0zvR3zt6Gykjw5beohhxIjeEHwa/Nn6MtCPENXSsBoumeXrqgdRvEqay0rlrS6AGqLRLujZ6NSLiS/GKZ+LFNLEmdYkQhueao8wjM5VVqFGiZ69tyh4vpRxeSaqCp4q0R98w9/zSmx/Buqy4W1oY5WVHwtVzVS6XmUlQrFKcXtmlZLOtdeeGia0s+B3F4LOAutchwf5KlhB61IAf1WUDTlPkneaYheMAMkPWXo1LQS/yJXsizEemowzFus4lYnk2W9grJqLxgW1CUgHqyYBUd9vDqKK5OyqBAtG299FoSDGkECn3Cs7o3ZWxly7WIDNUndmthGbFm2+FbuDLwrZ6l1fvyunKk3aZSPKjOfVujBlAMS5Qh/wTbZIhVG3iZuQY+OLudqeWT1Tu9enqxxm9QHmCwMhAjf3ggAI6nFuR0OjT9ZSYUODDQVuDEcm7TqJPENhxrkdDRVYoj1aLSlppCS4YSNLE5ywU7tAE3i0HeuUvc5k9b6ZVDK+qEUl9oFf16u5aK2hvyd5qj3Hwz1zGV+IIhNpbZ2gy7Val9bZOoabiFiuYGoXaki4Vte/4QD2biIWhWgOnpoSywJmVnHX8K7dNlv9XKjVu2zzCWxh7wDjYXPKcRkXMtcmh+YQ0S/EzqoSWXJICEn3Oe1OIHqsAz/AU2lowNHW1VIVpoqC+ACj9qJUrKBkQpUxL2OhLcxvTDGm8URq/geEqDaL2fWdwmD5oKkZo+RpvuS6YKuFTvmVKHowmP1+Uck+OIC9kQD8Nbe6zYWwZmHPCxc5bGe8qRdvAO0SbSfOwDMeXNfVf9lK3JaiWlTtYr0Ia+/u6QmMx6J0B17To+L14fy8FJUWkhgJSfjcYGKXHQ3L2RfFMnh2u4T2ZWTV5vpPAmasViueJSgzxeBHlV4tVObsyhOOtUMjTrSdIu5piC1+66pZh9CYQu4hliy2ZBwGyP9zy7Bmc0B7lmGjn3arfhKpoFS5gG6sNJmuqnOaufinTBJhytTh7arvANrVPfQGRvsBqbPcTvnkIYHnZgstxULP2oPEd9joww/6wAjZdU0b5jztomBNA4Jdfz+D3x988WdmHyltWpWrPJWxrFqLSbVtv8sqSLLCZJnrufNCiFwXLR+yTwXPSv2Cw9J0cvI9geanA7RXx0Bw4GhkoPZcyr4ZpOeng/SghZq4zKtjpBdG3Z/RVwt8P9v99IWyXWBT0POXYdj1DCvqhqNnSHf/UhVUtIezXYR/+N9/bSr76VrGe/M9z1X5j7tyW68qrh95lKM8WXHcw9b3cPeH1oVFtO8sRwJ+eg/gpw8HfnrywJOgro+Do2E9uwfWs4djPTsxrD2X9I05rMNJ0LsbsePV0jVCtqJuJ14P7oPVdffBuPsgbye63r6f0g5X3R3tHaX27mkc+0covZ/MPh9/2v1ipRcKcJ1aXcYCSv2AsoiGIfVHbwekKdFdHHXjB/mGCvYTU48u1nva8etu6WD4GBBoyiP27ahjfmLqAK8gfeBtod90r4E78kZfL/z9VPr2CyfRp6jfSft64Wne/PUT7G8Aiir2C5tumnx7LZmub0+MG7tlg/H683XwND0tOVzHwP2DkWjH6hFe0PmfQ+0HMS8qUUqe1Wm+gvlHrSsktvlenXiTsow3pAe6ra6+1jc1Wo9ut06sHtXvJIzm9Hvcfg/wDA5yE+bT2zGfPhbz6alivuckUR2Urif3o6lgdrsKZo9VwewkVfC8eeDWRutAu3Wg6bpX63WgATvQhh1oxj6/JTt2Y9Z8O+B6Dnvexuxz7PaJznyf9sxzPf3dPIb9yAswJXTXnfku+XZe6/OT1MoDuzLmkq/3ff8NLdmJaeSuxozqN5tfjwqG3e/BmG+O1d+Bfv1/UEsHCOse+Mv1BwAAoC0AAFBLAQIUABQACAAIACNe4UDWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAI17hQOse+Mv1BwAAoC0AAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAACMCAAAAAA=" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /><br /> | Falls nichts angezeigt wird, können Sie mit folgendem Link [{{fullurl:{{PAGENAME}}|action=purge}} den Servercache leeren].<br /><br /><ggb_applet width="624" height="445" version="4.0" ggbBase64="UEsDBBQACAAIACNe4UAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIACNe4UAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vrdcts2Fr5OnwLDi150IgogSFDMSulEajqbmbTJrLOdnd5BJCyhpgiWpGS504faZ9gn2wOApEhZ/o2tKPFYBkEc4uB855/W+MftKkUbUZRSZROHuNhBIotVIrPFxFlX54OR8+Pr78YLoRZiXnB0rooVryaOryllMnGimMbzkUgG0ZzhgY+pGMwpXDEcJOdRiMMIhw5C21K+ytSvfCXKnMfiLF6KFX+vYl4Zxsuqyl8Nh5eXl27DylXFYrhYzN1tmTgIjpmVE6e+eAXb9R66pIbcw5gM//PLe7v9QGZlxbNYOEiLsJavv3sxvpRZoi7RpUyq5cRh1HPQUsjFEmQK9EmHmigHQHIRV3IjSni0MzUyV6vcMWQ80+sv7BVKW3EclMiNTEQxcbBLCfODgEXMw14AE2CiCimyqiYmNdNhs914I8Wl3VdfGZa+gyql0jnXW6K//0awGUYv9UDs4MHAmF3C9h6mdvDs4NshsDS+fdy3pL6l8S2NTx20kaWcp2LinPO0BAhldl6A+tp5WV2lwpynvrETn7wEmUr5FxBTDHZiMYf7GL/UHwYfXy8M+0KSDteqWD+QacOSef79WXo3s7TTWzjShqPXFZIxED+gL73gBiHZLdjeybOVkgQdnsDK/JrPNY7UewBHO/88hsw/iojjYeMo49o3ULnUtLUiK7EqtbfQCAWRNnqCAvAMFoKNB4hEMIQeAl9AJEB+AFMyQkyPIaIhLPiIohHSdIQi4xrBCP74odmMoQA203dD8EhEgJGPAoqI8SgfgR8h45XgoR4FiiBAATyk2RNPb0EZ8hnM6Aj5cEbtkCEBQgoPwhzYe4gSRPXDJEQeQ0zvR3zt6Gykjw5beohhxIjeEHwa/Nn6MtCPENXSsBoumeXrqgdRvEqay0rlrS6AGqLRLujZ6NSLiS/GKZ+LFNLEmdYkQhueao8wjM5VVqFGiZ69tyh4vpRxeSaqCp4q0R98w9/zSmx/Buqy4W1oY5WVHwtVzVS6XmUlQrFKcXtmlZLOtdeeGia0s+B3F4LOAutchwf5KlhB61IAf1WUDTlPkneaYheMAMkPWXo1LQS/yJXsizEemowzFus4lYnk2W9grJqLxgW1CUgHqyYBUd9vDqKK5OyqBAtG299FoSDGkECn3Cs7o3ZWxly7WIDNUndmthGbFm2+FbuDLwrZ6l1fvyunKk3aZSPKjOfVujBlAMS5Qh/wTbZIhVG3iZuQY+OLudqeWT1Tu9enqxxm9QHmCwMhAjf3ggAI6nFuR0OjT9ZSYUODDQVuDEcm7TqJPENhxrkdDRVYoj1aLSlppCS4YSNLE5ywU7tAE3i0HeuUvc5k9b6ZVDK+qEUl9oFf16u5aK2hvyd5qj3Hwz1zGV+IIhNpbZ2gy7Val9bZOoabiFiuYGoXaki4Vte/4QD2biIWhWgOnpoSywJmVnHX8K7dNlv9XKjVu2zzCWxh7wDjYXPKcRkXMtcmh+YQ0S/EzqoSWXJICEn3Oe1OIHqsAz/AU2lowNHW1VIVpoqC+ACj9qJUrKBkQpUxL2OhLcxvTDGm8URq/geEqDaL2fWdwmD5oKkZo+RpvuS6YKuFTvmVKHowmP1+Uck+OIC9kQD8Nbe6zYWwZmHPCxc5bGe8qRdvAO0SbSfOwDMeXNfVf9lK3JaiWlTtYr0Ia+/u6QmMx6J0B17To+L14fy8FJUWkhgJSfjcYGKXHQ3L2RfFMnh2u4T2ZWTV5vpPAmasViueJSgzxeBHlV4tVObsyhOOtUMjTrSdIu5piC1+66pZh9CYQu4hliy2ZBwGyP9zy7Bmc0B7lmGjn3arfhKpoFS5gG6sNJmuqnOaufinTBJhytTh7arvANrVPfQGRvsBqbPcTvnkIYHnZgstxULP2oPEd9joww/6wAjZdU0b5jztomBNA4Jdfz+D3x988WdmHyltWpWrPJWxrFqLSbVtv8sqSLLCZJnrufNCiFwXLR+yTwXPSv2Cw9J0cvI9geanA7RXx0Bw4GhkoPZcyr4ZpOeng/SghZq4zKtjpBdG3Z/RVwt8P9v99IWyXWBT0POXYdj1DCvqhqNnSHf/UhVUtIezXYR/+N9/bSr76VrGe/M9z1X5j7tyW68qrh95lKM8WXHcw9b3cPeH1oVFtO8sRwJ+eg/gpw8HfnrywJOgro+Do2E9uwfWs4djPTsxrD2X9I05rMNJ0LsbsePV0jVCtqJuJ14P7oPVdffBuPsgbye63r6f0g5X3R3tHaX27mkc+0covZ/MPh9/2v1ipRcKcJ1aXcYCSv2AsoiGIfVHbwekKdFdHHXjB/mGCvYTU48u1nva8etu6WD4GBBoyiP27ahjfmLqAK8gfeBtod90r4E78kZfL/z9VPr2CyfRp6jfSft64Wne/PUT7G8Aiir2C5tumnx7LZmub0+MG7tlg/H683XwND0tOVzHwP2DkWjH6hFe0PmfQ+0HMS8qUUqe1Wm+gvlHrSsktvlenXiTsow3pAe6ra6+1jc1Wo9ut06sHtXvJIzm9Hvcfg/wDA5yE+bT2zGfPhbz6alivuckUR2Urif3o6lgdrsKZo9VwewkVfC8eeDWRutAu3Wg6bpX63WgATvQhh1oxj6/JTt2Y9Z8O+B6Dnvexuxz7PaJznyf9sxzPf3dPIb9yAswJXTXnfku+XZe6/OT1MoDuzLmkq/3ff8NLdmJaeSuxozqN5tfjwqG3e/BmG+O1d+Bfv1/UEsHCOse+Mv1BwAAoC0AAFBLAQIUABQACAAIACNe4UDWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAI17hQOse+Mv1BwAAoC0AAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAACMCAAAAAA=" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /><br /> | ||
| + | ===Lösung von AlanTu=== | ||
| + | Hier schonmal das Geogebra-Applet: | ||
| + | <ggb_applet width="900" height="900" version="4.0" ggbBase64="UEsDBBQACAgIAFwLOUoAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICABcCzlKAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbN1b227bRhq+Tp9iwIu9KCxqjjxk5RSxk2ADpE3QZIvFBkVBkWOZNUVyebDlog+1+wr7APtM+88MSZGSrEiK7SgJmvIw/5y+7z+OmMkPi3mCrmVRxll6ahEbW0imYRbF6ezUqquLkWf98Oy7yUxmMzktAnSRFfOgOrW4koyjU8sPWTj1ZDTypw4ecczkaMrgzsEiuvBd7PrYtRBalPHTNPspmMsyD0L5PryU8+BNFgaVnviyqvKn4/HNzY3dTmVnxWw8m03tRRlZCJaZlqdWc/MUhht0umFanGJMxv/48Y0ZfhSnZRWkobSQ2kIdP/vuyeQmTqPsBt3EUXUJq/dgcZcynl3CnlziWGishHIAJJdhFV/LErr2HvWeq3luabEgVe1PzB1Kuu1YKIqv40gWpxa2qcddTAjh3PMY94SFsiKWadXIkmbOcTva5DqWN2ZYdadn5BaqsiyZBmpE9OefiGKK0Ym6EHOhcHEc04TNO8zMhZoLNxdhZLjpzo0oNzLcyHBmoeu4jKeJPLUugqQEBOP0ogD2uueyuk2kXk/zYrl7cgJ7KuM/QJhhUBMDObzH+ET9deAvVw3j4SZJb9aqqPectJ1SU7rrlPSzNsraOalHlnM6Djmh2D8RrnPi+3R9m86WSc2+d9knET1oBT7R/+m/azOybdtcndE8f96EDn+ULU7GralMGutA5aWSbbSnkvNS2QvzkfCV2hMkwDYcF7RcIOLDxaUIrAERgbiAR+IhR11dxFxo4IghDyk5wpA2DuHB/7irB3OQgMHUWxdsEhGYiCPBENE2xRFYEtJ2CTZKGUgIgQR0UtMTqoZgDuIOPDEPcVijMkmXgCCDjvAM01PECGKqM3ERdZCjxiNcmbrjqaXDkBQ5GDlEDQhWDRZtrBnkPcTUblq3Fqd5XQ0gCudRe1tleccFSIM/Wno9458GTvHJJAmmMoE48V4xidB1kCiL0BNdZGmFWhKpeTcrgvwyDsv3sqqgV4l+D66DN0ElF69Aumzn1rJhlpbviqw6z5J6npYIhVmCuzVnCend027V8MB6DbzfIHoNTu/e3ThvBi2oLiXMnxVlKx5E0WslsXQNgOTbNLk9K2RwlWfxcBuTsQ45E1mHSRzFQfoLKKuaReGCNkYgAX6kWUhWRO9vS9BgtPinLDKAlgibU8EEpS4lTKhAcmuaOBe2cFwC/tvxqeMC32UYKNtzsY2ho0OxABfocQ/6bG5yPDOzvO4IChay2/usiKP+/evyLEuiDgm9+fMgr+pCZw7gGQu1pefpLJFaQbSvhbAcXk2zxXujGcyM9eE2hyds5p/ONOgIHAMVsMVZc52aq5ZRC+uksJbBWgK3qhZHXTtRLnjWXKfmqqVAd83Smo2SdpcEt9PEpXZn2BoYjVZ8FeTrNK7etA9VHF41OyVG/qd6PpWd+gyHJPc05GS8ol6TK1mkMmm0GYiss7o0xtlT9EiG8RweTUMDSKDI+jsswLyN5KyQ7boTnZMZuHQr7ivq2ms91Ksim79Orz+AJqwsYDJuVzkpwyLOlb6hKUSAK7nUqSguAwggUb+fMj/YeqgCBcBTKWie1xczQAxctM3egZXW1WUGvD9PgvRDDcOAiwEwlSEmcg55F6q0vmmV7ZB/rhM6BTHKpr+Dl1thZkkhNG/UPa2lQZJfBirpa3BIgltZDJDR4/2YRat4AR16U2DyuaE7l9Ioilkv3OQwnDavgcsCAkq0OLVGVOXkt01u/ofJ5k06q7aqbG7gpM3bFepAnwxKn8Dr7FHxentxUcpKbZLoHRL3ocHEtvNoWJ5/USzFg+sltplnaLP5vYAZZvN5kEYo1fnkuyy5nWWptcxwAqwMGgVE6SkKqILY4FdXbTt4ywSCETFioREL4AIpxNRM2EyzgT0zYctPN9QwqlSQ7VxBSVfq0Fc1QU7f/C2OIqkz3fF26nuA9rkngmn2BWnC3pJ8so/juVtDSzlTT91Cwk/o6P4L3dND9k3TuDmqTBS0aUQw6NX4UPDlv1LTpTSRNp7nSRzGVacxidLt12kFcVfqwLMeTq+kzFUW8zb9UARpqQ5JjEwvTO8IdHA8QNPGB4IB+56GmtrM+WaQnh4P0qMOamI7tPGR1PX7f7yvFvhhtHvxhaKdMCHo4dMwbFM9FbNd7wHC3c9ZBRnt5mjn4+//+28Tyl6sRbznfwnyrPzrp2LbICtuuhxkKPeWHA+w5RT3/7AmsfBXjeWRgD/bAfiz/YE/O3rgiWjyY/FoWJ/vgPX5/lifHxnW1CZDZXYbdyIGb33n8XLpBiGTUXcPdAD3xuy63zHsdwy6B5Vv70ba5qy7x96j5N4DxjF/hNT73vTz8NWuJisDV4Cb0Go7jmCMC+b4zHUZ916OSJui29jv+w/yDSXsR0aPStYH7PCmWtroPkYEinLf+XbomB4ZHWAVZAi8SfTb6lXYHvW+XviHofTlFw6i95G/k+544X5O/oYB9hcAJStWE5t+mHy5Fkzr7YHx2gzZYlx/Pgf3U9OSzXkMvN/oiZZTHWAFvZ8hGjsIg6KSZRykTZiv4Pmd4grJRb6SJ95FlraGZEO11eervqvQOrjcOrJ8VJ1JaObUOe6wBngAA7kL87PtmJ8divnZsWK+YiR+45TWg/ujUXC+nYLzQyk4P0oKHjYObC20NpRbG4qunUqvDQXYhjJsQzH2+SXZYxdm7ecC6zHsYQuzz9Hbe1rzLuUZtan6wM/B3KcCM8KW1Rm3ybdzrB8cJSt7VmWOTb7e8/47SrIjY+RThRlTJ5tfDwXD8PK2qC4zcM1B8gYWvxJlXtwVwcvf6HaHr5DoqFLS28nc/FOO+uGs91XXvRQbd9Qad5QaIyi6SZ98T+zCtDry3pPqPU+4dYHyEYD91VDExZaj7lf75FivDqKKUGN2+nq/J9yucHzsCeExzonX/JZAmE8xUd8pupQR/wHyLv1B4grqhoqPHfgnCNv01xPEiIL/BL1o2HhhmFiRW+Plf//ZToz+Nq4DHqRVf1h73e7Adj3BfI84jPku557zqYRo20+mBB/uM8nh/i8owh5V7fFMkmQ3P8uLRC40D7t6sw0+bHfO1p0c2cvJkaNxclD8gTIwQcF4uOtj2lTlnMOjq74K5q6gnPDlmTsHQ8OMUexhB7uH03mYj7urkFSRQ7NjTsM+Ylug71G9bkrlb2wvrtjRcLVnQGK2x0S/wwOdCN/NVZeKrHHVfCLXcDEMQfEir9Oraq9I1PY5FqqgKyc+JYJRh/qcMtflzbciNoYGDm89zqjLNFcQpXrCov3pZCU6ic3RiaySMO5/0az/zUDzz9+e/R9QSwcIxxmP4rIJAACbNwAAUEsBAhQAFAAICAgAXAs5SkXM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICABcCzlKxxmP4rIJAACbNwAADAAAAAAAAAAAAAAAAABeAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAEoKAAAAAA==" showResetIcon = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "true" showAlgebraInput = "true" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| + | Beschreibung liefere ich nach, nur schonmal so viel: <math>S_{s_1} \circ S_{s_2}</math> beschreibt die erste Abbildung (die Drehung), <math>S_{s_2} \circ S_{s_3}</math> beschreibt die zweite Abbildung (die Translation). | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Version vom 25. Januar 2017, 01:30 Uhr
Das Dreieck  wird an Punkt D um 90 gedreht. Das gedrehte Dreieck wird nun um den eingezeichneten Vektor verschoben. Gibt es einen Punkt der Ebene, der nun genau wieder an seinem ursprünglichen Ort liegt? Konstruieren Sie ggf. diesen Punkt und begründen Sie!
wird an Punkt D um 90 gedreht. Das gedrehte Dreieck wird nun um den eingezeichneten Vektor verschoben. Gibt es einen Punkt der Ebene, der nun genau wieder an seinem ursprünglichen Ort liegt? Konstruieren Sie ggf. diesen Punkt und begründen Sie!
Falls nichts angezeigt wird, können Sie mit folgendem Link den Servercache leeren.
Lösung von AlanTu
Hier schonmal das Geogebra-Applet:
Beschreibung liefere ich nach, nur schonmal so viel: 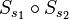 beschreibt die erste Abbildung (die Drehung),
beschreibt die erste Abbildung (die Drehung), 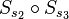 beschreibt die zweite Abbildung (die Translation).
beschreibt die zweite Abbildung (die Translation).

