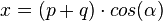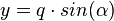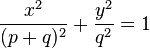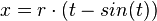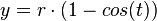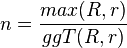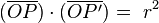Anregungen: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 8: | Zeile 8: | ||
<math>x=(p+q)\cdot cos(\alpha)</math><br/> | <math>x=(p+q)\cdot cos(\alpha)</math><br/> | ||
<math>y=q \cdot sin(\alpha)</math><br/><br/> | <math>y=q \cdot sin(\alpha)</math><br/><br/> | ||
| − | |||
Hierbei ist p die Strecke <math>\overline{AB}</math> und q die Strecke <math>\overline{BC}.</math> Nun was kann man mit diesem Gerät machen? <br/> | Hierbei ist p die Strecke <math>\overline{AB}</math> und q die Strecke <math>\overline{BC}.</math> Nun was kann man mit diesem Gerät machen? <br/> | ||
Es handelt sich hier um einen <u>Ellipsograph</u>. Neben der ''Gärtnerkonstruktion'', kann man mit diesem Gerät eine Ellipse konstruieren. <br/><br/> | Es handelt sich hier um einen <u>Ellipsograph</u>. Neben der ''Gärtnerkonstruktion'', kann man mit diesem Gerät eine Ellipse konstruieren. <br/><br/> | ||
Version vom 31. Januar 2017, 02:31 Uhr
Trammel of Archimedes / Ellipsenzirkel
GeoGebra Applet wird nicht angezeigt?
[ www.geogebra.org is not an authorized iframe site ]
Copyright by Ryan Hirst (GeoGebra Material)
Sei C der äußere Punkt des Hebels, sowie Punkt A und Punkt B Schieber innerhalb der Konstruktion, wobei sich A entlang der y-Achse und B entlang der x-Achse bewegt.
Weiterhin seider Winkel, der zwischen der x-Achse und der Halbgeraden
entsteht (wobei B der Scheitel ist). Dann gilt für die Koordinaten von C folgende Parameterform:
Hierbei ist p die Streckeund q die Strecke
Nun was kann man mit diesem Gerät machen?
Es handelt sich hier um einen Ellipsograph. Neben der Gärtnerkonstruktion, kann man mit diesem Gerät eine Ellipse konstruieren.
Durch Umformen (mittels Satz des Pythagoras,) erhalten wir:
Dies ist eine Ellipsengleichung.
Es lassen sich noch andere, geometrische Objekte aus dem Trammel of Archimedes / Ellipsenzirkel definieren, bspw. eine Hypozykloide (betätige den Button rolling circle). --Tutor: Alex (Diskussion) 17:59, 23. Dez. 2016 (CET)
Zykloide
[ www.geogebra.org is not an authorized iframe site ]
Eine Zykloide ist die Ortslinie/Bahn, die ein Kreispunkt beim Abrollen eines Kreises auf einer Leitkurve beschreibt.
Schon wie oben erwähnt und gezeigt kann man diesen Kreis nicht nur auf Geraden, sondern auch auf Kreisen selbst, innerhalb oder außerhalb abrollen lassen.
Lässt man den Kreis außen auf einem anderen Kreis abrollen, so entsteht eine Epizykloide. Rollt man den Kreis jedoch im Inneren eines Kreises ab, so entsteht eine Hypozykloide.
Verschiedene Ortskurven lassen sich bilden, wenn man in der GeoGebra Applet den Radius des abrollenden Kreises und den Radius des großen Kreises ändert. Dabei gelten spezielle Verhältnisse um Schleifen zu bilden.
Bspw. beträgt der Radius des großen Kreises R=6 und der Radius des abrollenden Kreises r=1.5, so entstehen 4 Schleifen. Bei dem Trammel of Archimedes ist R=6 und r=3.
In meiner selbst erstellten GeoGebra Applet könnt Ihr experimentieren.
Sei P der Punkt, der die Hypozykloide bildet, so gilt folgende Parameterform für dessen Koordinaten:
Hierbei ist r der Radius des Kreises und t der Parameter (Wälzwinkel).
Möchte man eine gewissen Anzahl an n Schleifen, gilt folgendes Verhältnis:
Dabei ist R der Radius des großen Kreises und r der, des abrollenden Kreises. So istdas Maximum der zwei Radien und der
, größte gemeinsame Teiler beider Radien.
Für was sind Zykloiden gut? Heutzutage nutzt man Zykloiden als Modelle in der Getriebetechnik. Dabei sollen Verzahnungen von mehreren Zahnrädern und Zahnstangen simuliert werden.
Aber auch schon im 16. Jahrhundert nutzte man sie für erste Flächen- und Längenberechnungen oder zur Konstruktion von Ellipsen. Weiterhin konnte man Planetenbahnen in unserem Sonnensystem vereinfacht darstellen. --Tutor: Alex (Diskussion) 22:28, 1. Jan. 2017 (CET)
Was ein Zufall, am Samstag erst ist ein Video zu einer Anwendung von Zykloiden erschienen, als Zusammenarbeit des Youtube-Channels vSauce und Adam Savage (bekannt aus „MythBusters“):
[ www.youtube.com is not an authorized iframe site ]
Darin zeigen Sie, dass man mithilfe von Zykloiden eine Lösung zum Brachistochrone-Problem finden kann. Ein Brachistochrone ist der schnellste Weg für eine Kugel um von A nach B zu rollen, wobei B natürlich niedriger als A liegt. Sie lösen das Problem, indem Sie einen Kreis auf einer Geraden abrollen. Auf diese Weise erhält man ein Brachistochrone, das zudem noch ein Tautochrone ist, ein Objekt benötigt also immer die selbe Menge an Zeit, um zum Tiefpunkt der Kurve zu gelangen. Ganz nebenbei werden auch noch Unterarten von Zykloiden erklärt (Trochoide, Epi- und Hypozykloide). Hier übrigens noch ein Geogebra-Applet von mir, als Demonstration wie man mit Zykloiden Ellipsen (oder verschiedene andere Figuren) konstruieren kann. --AlanTu (Diskussion) 19:15, 23. Jan. 2017 (CET)
Hallo AlanTu,
dein Beitrag zu Zykloiden, sowie deine GeoGebra-Applikation sind klasse ;)
Ich freue mich sehr, dass diese Seite dich (euch Studenten) anregt, eine andere Sichtweise auf die Geometrie zu erhalten, nebst dem, was in den Vorlesungen, Seminaren, ... geboten wird. Jeden Monat (bis zur vorlesungsfreien Zeit) möchte ich Euch eine andere Besonderheit der Geometrie nahebringen, die Ihr so, nur in Teilen oder vllt. nicht im Studium analysiert.
Um jeden Beitrag und jede Erweiterung bin ich und auch die anderen Studenten dankbar.
Weiter so!
Gruß --Tutor: Alex (Diskussion) 02:18, 24. Jan. 2017 (CET)
Inversion am Kreis
[ www.geogebra.org is not an authorized iframe site ]
Punkte kann man nicht nur an Geraden spiegeln. In meinem selbst erstellten GeoGebra Applet könnt Ihr einen Punkt am Kreis spiegeln.
In der ebenen Geometrie ist die Spiegelung am Kreis eine Abbildung die nur winkeltreu ist. Da diese Abbildung nicht einmal geradentreu ist, ist sie im Gegensatz zur Geradenspiegelung keine Kongruenzabbildung.
Bei einer Spiegelung am Kreis, mit Punktund Bildpunkt
, gilt stets folgende Bedingung:
Befindet sichim Inneren des Kreises, so erhält man
wie folgt: * Konstruiere die Halbgerade
* Konstruiere die Senkrechte auf
, die durch
geht * Der Inversionskreis bildet mit der Senkrechten zwei Schnittpunkte, konstruiere jeweils die Tangenten am Inversionskreis durch die Schnittpunkte * Der Schnittpunkt der beiden Tangenten mit der Halbgeraden
ist
Liegt der Punktjedoch im Äußeren des Kreises, so erhält man
wie folgt: * Bestimme den Mittelpunkt
der Strecke
und konstruiere einen Kreis
um
mit
*
schneidet den Inversionskreis in zwei Punkten, bilde deren Gerade * Diese Gerade schneitet die Strecke
, dies ist der Spiegelpunkt
Bewegt mannahe an den Mittelpunkt
des Inversionskreises, so gelangt dessen Bildpunkt ins unendlich Ferne. Bewegt man
jedoch nahe an den Rand des Inversionskreises, so liegt dessen Bildpunkt auch nahe an dem Rand des Inversionskreises. Liegt
auf dem Rand, so ist er ein Fixpunkt.
Natürlich kann man nicht nur Punkte, sondern auch geometrische Objekte der ebenen Geometrie am Kreis spiegeln, so wird aber bspw. aus einer Strecke, die gespiegelt wird, eine Kurve. --Tutor: Alex (Diskussion) 00:00, 01. Feb. 2017 (CET)