Stell deine Frage: Unterschied zwischen den Versionen
| Zeile 25: | Zeile 25: | ||
Hallo AlanTu,<br/> | Hallo AlanTu,<br/> | ||
bei einer ''Halbgeraden'' handelt es sich um ein geometrisches Objekt, das entsteht, wenn ein Punkt eine Gerade, auf der er liegt, teilt. | bei einer ''Halbgeraden'' handelt es sich um ein geometrisches Objekt, das entsteht, wenn ein Punkt eine Gerade, auf der er liegt, teilt. | ||
| − | Dabei ist der Punkt <u>wahlweise</u> Teil der Halbgeraden oder nicht. Neben der gängigen <math>AB^+</math> | + | Dabei ist der Punkt <u>wahlweise</u> Teil der Halbgeraden oder nicht. Neben der gängigen <math>AB^+</math> Schreibweise, |
gibt es in der analytischen Darstellung auch <math>[AB</math>, als halboffenes Intervall. Hierbei bildet dieses die Menge aller Punkte <math>X</math>, | gibt es in der analytischen Darstellung auch <math>[AB</math>, als halboffenes Intervall. Hierbei bildet dieses die Menge aller Punkte <math>X</math>, | ||
deren Ortsvektor <math>\vec{X}</math> gegeben ist durch:<br/> | deren Ortsvektor <math>\vec{X}</math> gegeben ist durch:<br/> | ||
Version vom 14. Februar 2017, 00:23 Uhr
Hier dürft Ihr gerne, noch offene mathematische Fragen stellen, die ich (Tutor: Alex) versuche zu beantworten.
Irrelevante Fragen, Fragen zur Klausur, o.Ä. wird gelöscht.
Um eine Frage zu stellen:
1) Log dich ein
2) Gehe auf der Seite hier, oben rechts, auf Bearbeiten
3) Stelle deine Frage am Ende des Beitrags
Inhaltsverzeichnis |
Notation von Geraden
Haben wir eine spezielle Notation für Geraden festgelegt? Für Strecken verwenden wir ja 
, für Halbgeraden 
bzw. 
. Oder sollen wir Strecken und Gerade auf die selbe Weise notieren, nur mit dem Zusatz „Gerade“ bzw. „Strecke“ vorne dran, also „Gerade “? --AlanTu (Diskussion) 17:44, 5. Feb. 2017 (CET)
Anmerkung: In der Schule haben meine Lehrer immer 
für Strecken und für Geraden verwendet, was ich immer ziemlich sinnvoll fand. Das wäre auch recht kompatibel mit der Schreibweise von Dreiecken als 
(im Sinne eines [geschlossenen] Streckenzugs, der die Punkte verbindet). --AlanTu (Diskussion) 22:04, 9. Feb. 2017 (CET)
Korrekt AlanTu,
für Strecken verwenden wir
Gruß --Tutor: Alex (Diskussion) 00:12, 14. Feb. 2017 (CET)
Halbgeraden inklusive oder exklusive Ursprung?
Auf der Seite Diskussion:Winkel, Innere eines Winkels, Nebenwinkel, Scheitelwinkel WS 16 17 hatte ich auch mal die Frage gestellt, ob der Startpunkt zur Halbgeraden gehört oder nicht. Insbesondere wichtig, wenn man z.B. einen Winkel als Vereinigung schreiben möchte (reicht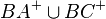 
oder muss man schreiben 
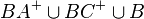, weil 
nicht zu den Schenkeln gehört). Für die genaue Fragestellung siehe die Diskussionsseite, wo ich die Frage ursprünglich gestellt hatte. --AlanTu (Diskussion) 17:12, 6. Feb. 2017 (CET)
Off-topic: Die ganzen Bilder aus den Classroompresenter-Übungen, die unter https://www.ph-heidelberg.de/wp/gieding/uebungen/ zu finden waren, wurden vom Server gelöscht oder zumindest verschoben und sind deshalb auch hier im Wiki nicht mehr sichtbar.
Hallo AlanTu,
bei einer Halbgeraden handelt es sich um ein geometrisches Objekt, das entsteht, wenn ein Punkt eine Gerade, auf der er liegt, teilt. Dabei ist der Punkt wahlweise Teil der Halbgeraden oder nicht. Neben der gängigen, als halboffenes Intervall. Hierbei bildet dieses die Menge aller Punkte
, deren Ortsvektor
gegeben ist durch:
mit
.
Eindeutig sieht man, dass wenn,
ist. Somit muss
als Startpunkt einer Halbgeraden
Möchte man den Anfangspunkt ausschließen, so handelt es sich um eine offene Halbgerade.
Gruß --Tutor: Alex (Diskussion) 00:12, 14. Feb. 2017 (CET)
