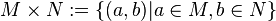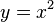Elementare Funktionen: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Kreuzprodukt zweier Mengen) |
*m.g.* (Diskussion | Beiträge) (→Kreuzprodukt zweier Mengen) |
||
| Zeile 3: | Zeile 3: | ||
==Kreuzprodukt zweier Mengen== | ==Kreuzprodukt zweier Mengen== | ||
Es seien M und N zwei nicht leere Mengen.<br /> | Es seien M und N zwei nicht leere Mengen.<br /> | ||
| − | Unter dem Kreuzprodukt MxN versteht man die mnge aller geordenten Paare (a,b) mit a aus M und b aus N. | + | Unter dem Kreuzprodukt MxN versteht man die mnge aller geordenten Paare (a,b) mit a aus M und b aus N.<br /> |
| − | <math>M \times N := \{(a,b)|a \in M, b \in N\}</math> | + | |
| + | <math>M \times N := \{(a,b)|a \in M, b \in N\}</math><br /> | ||
| + | <math>y=x^2</math> | ||
==Relationen== | ==Relationen== | ||
Version vom 15. Februar 2017, 15:33 Uhr
Inhaltsverzeichnis |
Der Funktionsbegriff
Elemente der Mengenlehre
Kreuzprodukt zweier Mengen
Es seien M und N zwei nicht leere Mengen.
Unter dem Kreuzprodukt MxN versteht man die mnge aller geordenten Paare (a,b) mit a aus M und b aus N.