Übungsaufgabe zur Vorbereitung: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 6: | Zeile 6: | ||
# Beweisen Sie: <math>\Phi = \frac{1 + \sqrt{5}}{2}</math> . | # Beweisen Sie: <math>\Phi = \frac{1 + \sqrt{5}}{2}</math> . | ||
# Beweisen Sie, dass eine Diagonale des regelmäßigen Fünfecks zu dessen Seitenlänge im Verhältnis des Goldenen Schnittes steht. Sie dürfen die oben angegebene Aussage zum Schnitt zweier Diagonalen eines solchen Fünfecks als wahr voraussetzen. | # Beweisen Sie, dass eine Diagonale des regelmäßigen Fünfecks zu dessen Seitenlänge im Verhältnis des Goldenen Schnittes steht. Sie dürfen die oben angegebene Aussage zum Schnitt zweier Diagonalen eines solchen Fünfecks als wahr voraussetzen. | ||
| − | # Das Fünfeck in ''Abbildung 1'' hätte auch durch eine zentrische Streckung an <math>\ M</math> aus dem Fünfeck generiert werden können. Bestimmen Sie den Streckfaktor dieser zentrischen Streckung.<br />Bemerkungen: Sie dürfen das Verhältnis des Goldenen Schnittes hinsichtlich Diagonalen- und Seitenlängen im regelmäßigen Fünfeck voraussetzen. Die Suche nach geeigneten Strahlensatzfiguren kann bei der Lösung des Problems hilfreich sein. | + | # Das Fünfeck <math>overline{A'B'C'D'E'}</math> in ''Abbildung 1'' hätte auch durch eine zentrische Streckung an <math>\ M</math> aus dem Fünfeck <math>overline{ABCDE}</math> generiert werden können. Bestimmen Sie den Streckfaktor dieser zentrischen Streckung.<br />Bemerkungen: Sie dürfen das Verhältnis des Goldenen Schnittes hinsichtlich Diagonalen- und Seitenlängen im regelmäßigen Fünfeck voraussetzen. Die Suche nach geeigneten Strahlensatzfiguren kann bei der Lösung des Problems hilfreich sein. |
# Beweisen Sie, dass sich die Diagonalen eines regelmäßigen Fünfecks wirklich im Verhältnis des Goldenen Schnittes teilen. | # Beweisen Sie, dass sich die Diagonalen eines regelmäßigen Fünfecks wirklich im Verhältnis des Goldenen Schnittes teilen. | ||
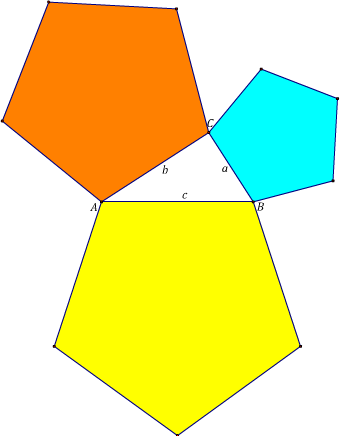
# Wie beim Quadrat ist der Flächeninhalt des regelmäßigen Fünfecks proportional zum Quadrat der Seitenlänge. Formulieren und beweisen Sie einen „Satz des Pythagoras“ entsprechend ''Abbildung 2''. Den üblichen Satz des Pythagoras dürfen Sie als bewiesen voraussetzen. | # Wie beim Quadrat ist der Flächeninhalt des regelmäßigen Fünfecks proportional zum Quadrat der Seitenlänge. Formulieren und beweisen Sie einen „Satz des Pythagoras“ entsprechend ''Abbildung 2''. Den üblichen Satz des Pythagoras dürfen Sie als bewiesen voraussetzen. | ||
Version vom 11. Juli 2010, 15:59 Uhr
Eine Strecke möge durch den Punkt derart in zwei Teilstrecken zerlegt werden, dass die längere der beiden Teilstrecken ist. Man spricht davon, dass der Punkt die Strecke im Verhältnis des Goldenen Schnittes teilt, wenn gilt. Man bezeichnet dieses Verhältnis mit dem griechischen Buchstaben 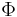 .
.
Es ist bekannt, dass sich zwei Diagonalen des regelmäßigen Fünfecks im Verhältnis des Goldenen Schnittes teilen.
- Formulieren Sie eine Konstruktionsbeschreibung zur Generierung eines regelmäßigen Fünfecks mit der Seitenlänge der Einheitsstrecke und begründen Sie Ihre Beschreibung.
- Beweisen Sie:
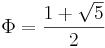 .
.
- Beweisen Sie, dass eine Diagonale des regelmäßigen Fünfecks zu dessen Seitenlänge im Verhältnis des Goldenen Schnittes steht. Sie dürfen die oben angegebene Aussage zum Schnitt zweier Diagonalen eines solchen Fünfecks als wahr voraussetzen.
- Das Fünfeck
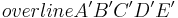 in Abbildung 1 hätte auch durch eine zentrische Streckung an
in Abbildung 1 hätte auch durch eine zentrische Streckung an  aus dem Fünfeck
aus dem Fünfeck 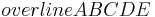 generiert werden können. Bestimmen Sie den Streckfaktor dieser zentrischen Streckung.
generiert werden können. Bestimmen Sie den Streckfaktor dieser zentrischen Streckung.
Bemerkungen: Sie dürfen das Verhältnis des Goldenen Schnittes hinsichtlich Diagonalen- und Seitenlängen im regelmäßigen Fünfeck voraussetzen. Die Suche nach geeigneten Strahlensatzfiguren kann bei der Lösung des Problems hilfreich sein. - Beweisen Sie, dass sich die Diagonalen eines regelmäßigen Fünfecks wirklich im Verhältnis des Goldenen Schnittes teilen.
- Wie beim Quadrat ist der Flächeninhalt des regelmäßigen Fünfecks proportional zum Quadrat der Seitenlänge. Formulieren und beweisen Sie einen „Satz des Pythagoras“ entsprechend Abbildung 2. Den üblichen Satz des Pythagoras dürfen Sie als bewiesen voraussetzen.