Implikationen SoSe 2017: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Begriff der Aussage) |
*m.g.* (Diskussion | Beiträge) (→Wichtige Sätze der Schulgeometrie) |
||
| Zeile 28: | Zeile 28: | ||
*Starker Außenwinkelsatz: Jeder Außenwinkel eines Dreiecks ist so groß wie die Summe der beiden nichtanliegenden Innenwinkel des Dreiecks. | *Starker Außenwinkelsatz: Jeder Außenwinkel eines Dreiecks ist so groß wie die Summe der beiden nichtanliegenden Innenwinkel des Dreiecks. | ||
*Basiswinkelsatz: Wenn ein Dreieck gleichschenklig ist, dann sind seine Basiswinkel kongruent zueinander. | *Basiswinkelsatz: Wenn ein Dreieck gleichschenklig ist, dann sind seine Basiswinkel kongruent zueinander. | ||
| + | Ergänzen Sie durch eigene Sätze, die Sie noch aus der Schule kennen: | ||
| + | * ..... | ||
| + | * ..... | ||
| + | * ..... | ||
==Begriff der Aussage== | ==Begriff der Aussage== | ||
Version vom 7. Mai 2017, 13:25 Uhr
Mathematische AussagenBeispielePrimzahlenEs lassen sich z.B. die folgenden Aussagen zu Primzahlen machen:
Keine Aussage zu Primzahlen ist:
Wichtige Sätze der SchulgeometrieSätze sind Aussagen, die wahr sind. Eine Aussage, die nicht wahr ist, kann demzufolge auch kein Satz sein.
Ergänzen Sie durch eigene Sätze, die Sie noch aus der Schule kennen:
Begriff der AussageEin sauber Definition des Begriffs mathematische Aussage bleibt uns hier versagt, es reichen intuitive Vorstellungen der folgenden Art:
Bei einer mathematischen Aussage setzt man zwei Prinzipien voraus:
Beide Prinzipien zusammengefasst:
Weitere Beispiele und Gegenbeispiele für AussagenErgänzen Sie die folgende Tabelle:
|
 ist eine Primzahl.
ist eine Primzahl.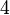 ist eine Primzahl.
ist eine Primzahl. nicht definiert.
nicht definiert.

