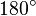Implikationen SoSe 2017: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Implikation 2: Teilbarkeit einer Summe) |
*m.g.* (Diskussion | Beiträge) (→Implikation 2: Teilbarkeit einer Summe) |
||
| Zeile 21: | Zeile 21: | ||
*Voraussetzung: <math>3|\overline{a}</math> | *Voraussetzung: <math>3|\overline{a}</math> | ||
*Behauptung: <math>3|a</math> | *Behauptung: <math>3|a</math> | ||
| − | === Implikation 2: Teilbarkeit | + | === Implikation 2: Satz zur Teilbarkeit von Summen=== |
:Für alle natürlichen Zahlen <math>a,b,t</math> gilt:<br /> | :Für alle natürlichen Zahlen <math>a,b,t</math> gilt:<br /> | ||
::Wenn <math>t</math> die Zahlen <math>a</math> und <math>b</math> teilt, dann teilt <math>t</math> auch die Summe <math>a+b</math>. | ::Wenn <math>t</math> die Zahlen <math>a</math> und <math>b</math> teilt, dann teilt <math>t</math> auch die Summe <math>a+b</math>. | ||
| Zeile 33: | Zeile 33: | ||
*Behauptung:<br /> | *Behauptung:<br /> | ||
::<math>t|(a+b)</math> | ::<math>t|(a+b)</math> | ||
| + | ===Implikation 3: Nebenwinkelsatz=== | ||
| + | :Wenn <math>\alpha</math> und <math>\beta</math> Nebenwinkel sind, dann ist die Summe ihrer Größen <math>180^\circ</math> | ||
| + | In anderer Formulierung ohne wenn-dann: | ||
| + | :Nebenwinkel ergänzen sich zu <math>180^\circ</math> | ||
| + | *Voraussetzung: | ||
| + | :: <math>\alpha</math> und <math>\beta</math> sind Nebenwinkel | ||
| + | *Behauptung: | ||
| + | ::<math>\alpha</math> und <math>\beta</math> sind supplementär. | ||
| + | ===Implikation 4: Scheitelwinkelsatz=== | ||
| + | :Wenn die beiden Winkel <math>\alpha</math> und <math>\beta</math> Scheitelwinkel sind, dann haben sie dieselbe Größe. | ||
| + | alternative Formulierung ohne wenn-dann: | ||
| + | :Scheitelwinkel haben dieselbe Größe. oder | ||
| + | :Scheitelwinkel sind kongruent zueinander. | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
|} | |} | ||
</div> | </div> | ||
[[Kategorie:Einführung_S]] | [[Kategorie:Einführung_S]] | ||
Version vom 10. Mai 2017, 15:56 Uhr
ImplikationenGenerelle Kennzeichnung von ImplikationenImplikationen sind spezielle mathematische Aussagen, deren Typ sich kurz als wie folgt darstellen bzw. beschreiben lässt:
Die Aussage BeispieleImplikation 1: Teilbarkeit durch 3
Implikation 2: Satz zur Teilbarkeit von Summen
Implikation 3: Nebenwinkelsatz
In anderer Formulierung ohne wenn-dann:
Implikation 4: Scheitelwinkelsatz
alternative Formulierung ohne wenn-dann:
|
 dann
dann  .
.

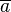 einer natürlichen Zahl
einer natürlichen Zahl  teilbar ist, dann ist auch die Zahl
teilbar ist, dann ist auch die Zahl 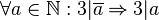
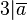
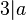
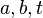 gilt:
gilt: die Zahlen
die Zahlen 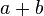 .
.
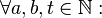
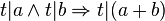
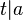
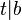
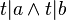
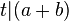
 und
und  Nebenwinkel sind, dann ist die Summe ihrer Größen
Nebenwinkel sind, dann ist die Summe ihrer Größen