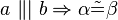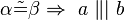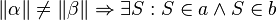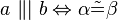Lösung von Aufgabe 4.03 S SoSe 17: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Lösung 1)
K (→‎Lösung 1)
Zeile 10: Zeile 10:
 
#<math>\ a \ \|| \ b \Leftrightarrow \alpha \tilde {=} \beta </math><br />
 
#<math>\ a \ \|| \ b \Leftrightarrow \alpha \tilde {=} \beta </math><br />
 
==Lösung 1==
 
==Lösung 1==
−
a) Es seinen zwei Parallelen geschnitten durch eine Gerade. Winkel α ist an der selben Setlle, also am Stufenwinkel, der Parallele kongruent.
+
1. Stufenwinkelsatz: Es seinen zwei Parallelen geschnitten durch eine Gerade. Winkel α ist an der selben Stelle, also am Stufenwinkel, der Parallele kongruent.
 +
 
 +
 
 +
2. Umkehrung Stufenwinkelsatz
  
 
==Lösung 2==
 
==Lösung 2==

Version vom 18. Mai 2017, 16:52 Uhr

Aufgabe 4.03

a) Wie lautet der Stufenwinkelsatz? (schauen Sie bei Bedarf in Schulbüchern nach).
b) Es seien a und b zwei nichtidentische Geraden, die durch eine dritte Gerade c jeweils in genau einem Punkt S geschnitten werden. Bei diesem Schnitt entstehen die Stufenwinkel \alpha und \beta . Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äuivalente Aussage (Begründen Sie jeweils)?

  1. \ a \ \|| \ b \Rightarrow \alpha \tilde {=} \beta
  2. \alpha \tilde {=} \beta \Rightarrow \ a \ \|| \ b
  3. \|\alpha \|\not= \| \beta \| \Rightarrow \exists S: S \in a \wedge S \in b
  4. \ a \ \|| \ b \Leftrightarrow \alpha \tilde {=} \beta

Lösung 1

1. Stufenwinkelsatz: Es seinen zwei Parallelen geschnitten durch eine Gerade. Winkel α ist an der selben Stelle, also am Stufenwinkel, der Parallele kongruent.


2. Umkehrung Stufenwinkelsatz

Lösung 2
Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_4.03_S_SoSe_17&oldid=29807“

Navigationsmenü