Lösung von Aufgabe 1.2 (SoSe 17): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
Zeile 24: Zeile 24:
 
  Zu deiner Aussage, dass <math> M_4 = M_5 </math> folgenden Hinweis:<br/>
 
  Zu deiner Aussage, dass <math> M_4 = M_5 </math> folgenden Hinweis:<br/>
 
  Du hast schon richtig geschlossen, dass <math> x^2=2 </math> . Auch hier die Frage: Welches Element <math> x </math> , löst uns diese Gleichung?  
 
  Du hast schon richtig geschlossen, dass <math> x^2=2 </math> . Auch hier die Frage: Welches Element <math> x </math> , löst uns diese Gleichung?  
−
  (Wir müssen hier wurzelziehen, dann kommen wir schnell auf ein Problem in <math> \mathbb{Q} </math>).<br/>
+
  (Wir müssen hier wurzelziehen, dann kommen wir schnell zu einem Problem in <math> \mathbb{Q} </math>).<br/>
 
  Nur weil hier andere ''Grundmengen'' (<math> \mathbb{N} , \mathbb{Z}, \mathbb{Q} \ und \ \mathbb{R} </math>)  verwendet worden sind, schließt das nicht zwangsweise aus, dass  
 
  Nur weil hier andere ''Grundmengen'' (<math> \mathbb{N} , \mathbb{Z}, \mathbb{Q} \ und \ \mathbb{R} </math>)  verwendet worden sind, schließt das nicht zwangsweise aus, dass  
 
  bspw. <math> M_3=M_6 </math> gilt. (diese Behauptung ist im Übrigen richtig ;) )
 
  bspw. <math> M_3=M_6 </math> gilt. (diese Behauptung ist im Übrigen richtig ;) )

Version vom 31. Mai 2017, 17:19 Uhr

Geben Sie eine andere Schreibweise der folgenden Mengen an und prüfen Sie, welche Mengen identisch sind.

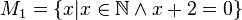
M_1 = \{x\vert x\in \mathbb{N}\wedge x+2 = 0\}

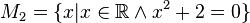
M_2 = \{x\vert x\in \mathbb{R}\wedge x^{2}+2 = 0\}

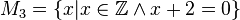
M_3 = \{x\vert x\in \mathbb{Z}\wedge x+2 = 0\}

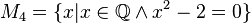
M_4 = \{x\vert x\in \mathbb{Q}\wedge x^{2}-2 = 0\}

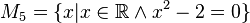
M_5 = \{x\vert x\in \mathbb{R}\wedge x^{2}-2 = 0\}

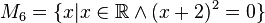
M_6 = \{x\vert x\in \mathbb{R}\wedge (x+2)^{2} = 0\}

Könnte man mir ein Beispiel zur anderen Schreibweise geben. Ich habe das Skript durchgearbeitet und die Videos, aber mir ist die andere Schreibweise noch nicht so klar. Ansonsten bin ich bei der Gleichheit der Mengen zur folgenden Ansicht gekommen: M4 = M5 da bei beiden x²=2 und Q und R sich nicht ausschließen. Alles andere sind nicht gleiche Mengen, da ihr Definitionsbereich es nicht zulässt. 

Hallo Kissa052,

ich werde versuchen dir die erste Menge ausführlich zu beschreiben. Ziel dieser Übung ist es sich mit der 
Mengenschreibweise auseinanderzusetzen, vertraut zu machen und einzelne Mengen untereinander zu vergleichen.
Dies machst du am besten, indem du die Elemente einer Menge beispielhaft, anhand der Vorschrift anschaust.

M_1 = \{x\vert x\in \mathbb{N}\wedge x+2 = 0\}

 bedeutet: Die Menge  M_1  enthält alle Elemente (alle Zahlen)  x , für die gilt,
 x \in \mathbb{N}  , sprich es soll eine Zahl aus den natürlichen Zahlen gewählt werden und (das ist dieses Zeichen \wedge) die Gleichung
 x+2 = 0  soll dabei erfüllt werden.

Jetzt die Frage: Kennst du ein Element / Elemente der natürlichen Zahlen, die uns diese Gleichung löst? Ich denke da gibt es keins, denn  \mathbb{N}:=\{0,1,2,3,4,...\}.
Das gesuchte Element ist  -2  , jedoch ist  -2 \notin \mathbb{N} . Somit gilt:  M_1= \empty  .

Zu deiner Aussage, dass  M_4 = M_5  folgenden Hinweis:

Du hast schon richtig geschlossen, dass  x^2=2  . Auch hier die Frage: Welches Element  x  , löst uns diese Gleichung? 
(Wir müssen hier wurzelziehen, dann kommen wir schnell zu einem Problem in  \mathbb{Q} ).

Nur weil hier andere Grundmengen ( \mathbb{N} , \mathbb{Z}, \mathbb{Q} \ und \ \mathbb{R} )  verwendet worden sind, schließt das nicht zwangsweise aus, dass 
bspw.  M_3=M_6  gilt. (diese Behauptung ist im Übrigen richtig ;) )
Das Wort Definitonsbereich steht im Zusammenhang mit Funktionen, was ich hier nicht verwenden würde.


Hoffe, dass ich dir helfen konnte. 
Versuche es und lass uns gerne an deinen Ergebnissen teilhaben, ich würde mich freuen ;) 
--Tutor: Alex (Diskussion) 17:23, 31. Mai 2017 (CEST)
Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_1.2_(SoSe_17)&oldid=29960“