Die symmetrische Gruppe S4 WS17/18: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→S_4) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 3: | Zeile 3: | ||
https://de.wikipedia.org/wiki/Symmetrische_Gruppe | https://de.wikipedia.org/wiki/Symmetrische_Gruppe | ||
| + | ==<math>S_3</math>== | ||
| + | Die <math>S_3</math> wäre dementsprechend die Gruppe aller Permutationen von 3 Elementen bzgl. der Nacheinanderausführung (NAF) von Abbildungen. Die <math>S_3</math> besteht damit aus <math>3!=6</math> Permutationen.<br /> | ||
| + | Eine Exceldatei zur Generierung der <math>S_3</math> wurde in der Vorlesung vorgestellt: <br /> | ||
| + | |||
==<math>S_4</math>== | ==<math>S_4</math>== | ||
| Zeile 11: | Zeile 15: | ||
Screenshot der Datei:<br /> | Screenshot der Datei:<br /> | ||
| − | [[Datei:S4 leer.png|screenshot der Exceldatei S4_leer]] | + | [[Datei:S4 leer.png|thumb|screenshot der Exceldatei S4_leer]] |
Version vom 31. Oktober 2017, 15:26 Uhr
Begriff der symmetrischen Gruppe 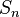
Unter einer symmetrischen Gruppe 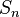 versteht man die Gruppe aller Permutationen von
versteht man die Gruppe aller Permutationen von  Elementen.
Elementen.
https://de.wikipedia.org/wiki/Symmetrische_Gruppe
Die 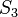 wäre dementsprechend die Gruppe aller Permutationen von 3 Elementen bzgl. der Nacheinanderausführung (NAF) von Abbildungen. Die
wäre dementsprechend die Gruppe aller Permutationen von 3 Elementen bzgl. der Nacheinanderausführung (NAF) von Abbildungen. Die 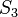 besteht damit aus
besteht damit aus 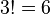 Permutationen.
Permutationen.
Eine Exceldatei zur Generierung der 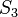 wurde in der Vorlesung vorgestellt:
wurde in der Vorlesung vorgestellt:
Die  wäre dementsprechend die Gruppe aller Permutationen von 4 Elementen bzgl. der Nacheinanderausführung (NAF) von Abbildungen. Die
wäre dementsprechend die Gruppe aller Permutationen von 4 Elementen bzgl. der Nacheinanderausführung (NAF) von Abbildungen. Die  besteht damit aus
besteht damit aus 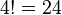 Permutationen.
Permutationen.
Datei:S 4 leer.xlsx
Screenshot der Datei:


