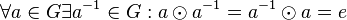Gruppendefinition (lang): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 2: | Zeile 2: | ||
{|width=90%| style="background-color:#CCFFCC; padding:1em" | {|width=90%| style="background-color:#CCFFCC; padding:1em" | ||
| valign="top" | | | valign="top" | | ||
| − | =Definition 1: (Algebraische Struktur)= | + | |
| + | =Definitionen= | ||
| + | ==Definition 1: (Algebraische Struktur)== | ||
Eine Menge <math>S</math> zusammen mit einer Operation <math>o</math> oder Relation <math>r</math> auf dieser Menge nennt man algebraische Struktur. <br /> | Eine Menge <math>S</math> zusammen mit einer Operation <math>o</math> oder Relation <math>r</math> auf dieser Menge nennt man algebraische Struktur. <br /> | ||
| Zeile 8: | Zeile 10: | ||
<math>[S, o]</math> bzw <math>[S, r]</math> | <math>[S, o]</math> bzw <math>[S, r]</math> | ||
| − | =Definition 2: (Halbgruppe)= | + | ==Definition 2: (Halbgruppe)== |
Eine algebraische Struktur <math>[H, \odot]</math> heißt Halbgruppe, wenn | Eine algebraische Struktur <math>[H, \odot]</math> heißt Halbgruppe, wenn | ||
<math>\odot</math> auf <math>H</math> abgeschlossen und assoziativ ist.<br /> | <math>\odot</math> auf <math>H</math> abgeschlossen und assoziativ ist.<br /> | ||
| Zeile 14: | Zeile 16: | ||
#(Abgeschlossenheit) <math>\forall a,b \in H: a \odot b \in H</math> | #(Abgeschlossenheit) <math>\forall a,b \in H: a \odot b \in H</math> | ||
#(Assoziativität) <math>\forall a, b, c: (a \odot b) \odot a = a \odot (b \odot c)</math>. | #(Assoziativität) <math>\forall a, b, c: (a \odot b) \odot a = a \odot (b \odot c)</math>. | ||
| − | =Definition 3: (Monoid)= | + | ==Definition 3: (Monoid)== |
Eine Halbgruppe <math>[M, \odot]</math> heißt Monoid, wenn sie ein Einselement hat:<br /> | Eine Halbgruppe <math>[M, \odot]</math> heißt Monoid, wenn sie ein Einselement hat:<br /> | ||
*(Einselement) <math>\exists e \in M \forall a \in M: e \odot a = a \odot e = a</math> | *(Einselement) <math>\exists e \in M \forall a \in M: e \odot a = a \odot e = a</math> | ||
| − | =Definition 4: (Gruppe)= | + | ==Definition 4: (Gruppe)== |
Ein Monoid <math>[G, \odot]</math> heißt Gruppe, wenn jedes Element von <math> G </math> in <math> G </math> ein inverses Element bzgl. <math>\odot</math> hat: | Ein Monoid <math>[G, \odot]</math> heißt Gruppe, wenn jedes Element von <math> G </math> in <math> G </math> ein inverses Element bzgl. <math>\odot</math> hat: | ||
*(inverse Elemente) <math>\forall a \in G \exist a^{-1} \in G: a \odot a^{-1}= a^{-1} \odot a = e</math> | *(inverse Elemente) <math>\forall a \in G \exist a^{-1} \in G: a \odot a^{-1}= a^{-1} \odot a = e</math> | ||
| + | =Bemerkungen= | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
|} | |} | ||
</div> | </div> | ||
[[Kategorie:Algebra]] | [[Kategorie:Algebra]] | ||
Version vom 5. November 2017, 17:00 Uhr
DefinitionenDefinition 1: (Algebraische Struktur)Eine Menge Schreibweise: Definition 2: (Halbgruppe)Eine algebraische Struktur
Definition 3: (Monoid)Eine Halbgruppe
Definition 4: (Gruppe)Ein Monoid
Bemerkungen |
 zusammen mit einer Operation
zusammen mit einer Operation 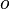 oder Relation
oder Relation  auf dieser Menge nennt man algebraische Struktur.
auf dieser Menge nennt man algebraische Struktur. ![[S, o]](/images/math/8/2/2/8222873ff784df1f8e8e2e6ac14800d4.png) bzw
bzw ![[S, r]](/images/math/8/9/e/89ec8cf7ec3eaea8e94ef96163bb1340.png)
![[H, \odot]](/images/math/b/5/0/b5051dd155dce8001fa2c6d3eec0868f.png) heißt Halbgruppe, wenn
heißt Halbgruppe, wenn
 auf
auf 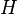 abgeschlossen und assoziativ ist.
abgeschlossen und assoziativ ist.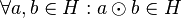
 .
.
![[M, \odot]](/images/math/1/b/7/1b76d279ea0a66347bff1d26e034943a.png) heißt Monoid, wenn sie ein Einselement hat:
heißt Monoid, wenn sie ein Einselement hat: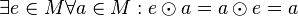
![[G, \odot]](/images/math/7/3/5/73557169bfbd888213d4a53d2c3ff1e4.png) heißt Gruppe, wenn jedes Element von
heißt Gruppe, wenn jedes Element von  in
in