Gruppendefinition (kurz): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Satz 2) |
*m.g.* (Diskussion | Beiträge) (→Beweis von Satz 2) |
||
| Zeile 30: | Zeile 30: | ||
==Beweis von Satz 2== | ==Beweis von Satz 2== | ||
Es sei <math>[G, \otimes]</math> Gruppe. Es gelte ferner für das Element <math>e \in G</math> die folgende Eigenschaft: <math>\forall g \in G: e \otimes g = g</math>.<br /> | Es sei <math>[G, \otimes]</math> Gruppe. Es gelte ferner für das Element <math>e \in G</math> die folgende Eigenschaft: <math>\forall g \in G: e \otimes g = g</math>.<br /> | ||
| − | Wir haben zu zeigen, dass jetzt auch <math>g \otimes e = g</math> für alle <math>g</math> aus <math>G</math> gilt. | + | Wir haben zu zeigen, dass jetzt auch <math>g \otimes e = g</math> für alle <math>g</math> aus <math>G</math> gilt.<br /> |
| + | Wir gehen von <math>(I) e \otimes g = g</math>.<br /> | ||
| + | In Gleichung <math>(I)</math> multiplizieren wir von rechts auf beiden Seiten mit <math>g^{-1}\otimes g</math> und erhalten <math>(II)</math>.<br /> | ||
| + | <math>(II) e \otimes g \otimes (g^{-1}\otimes g) = g \otimes (g^{-1}\otimes g)</math>.<br /> | ||
| + | Aus <math>(II)</math> folgt:<br /> | ||
| + | <math>(III) e \otimes g = g \otimes e</math> q,e.d. | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
|} | |} | ||
</div> | </div> | ||
[[Kategorie:Algebra]] | [[Kategorie:Algebra]] | ||
Version vom 25. November 2017, 12:13 Uhr
Linksinvers gleich RechtsinversSatz 1Es sei Beweis von Satz 1Es sei
Mit Gleichung (VI) haben wir gezeigt, dass das Linksinverse von Linkseins gleich RechtseinsSatz 2Es sei Beweis von Satz 2Es sei |
![[G, \odot]](/images/math/7/3/5/73557169bfbd888213d4a53d2c3ff1e4.png) eine Gruppe.
eine Gruppe.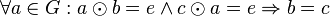
 das Linksinverse bzgl.
das Linksinverse bzgl.  von
von  .
. 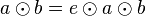
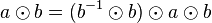
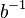

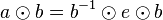
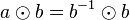
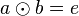
![[G, \otimes]](/images/math/0/1/3/01322720752789c5d9651172aee2d990.png) eine Gruppe. Wenn
eine Gruppe. Wenn 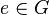 von links multipliziert Einselement von
von links multipliziert Einselement von  auch von rechts multipliziert Einselement von
auch von rechts multipliziert Einselement von  .
.
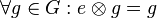 .
.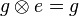 für alle
für alle  aus
aus 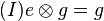 .
.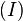 multiplizieren wir von rechts auf beiden Seiten mit
multiplizieren wir von rechts auf beiden Seiten mit 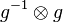 und erhalten
und erhalten 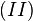 .
.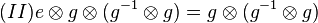 .
.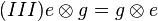 q,e.d.
q,e.d.

