Umkehrung von Implikationen SoSe 2018: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Implikation) |
*m.g.* (Diskussion | Beiträge) (→Beispiel 1) |
||
| Zeile 8: | Zeile 8: | ||
Beide Implikationen, Ausgangsimplikation und zugehörige Umkehrung, müssen nicht zwangsläufig denselben Wahrheitsgehalt haben. | Beide Implikationen, Ausgangsimplikation und zugehörige Umkehrung, müssen nicht zwangsläufig denselben Wahrheitsgehalt haben. | ||
=Beispiele= | =Beispiele= | ||
| − | ==Beispiel 1== | + | ==Beispiel 1 Teilbarkeit== |
| − | ===Implikation=== | + | ===Implikation: Aus der Teilbarkeit durch 9 folgt die Teilbarkeit durch 3=== |
Wenn eine Zahl <math>9</math> ein Teiler von <math>a</math> ist, dann ist <math>3</math> auch ein Teiler von <math>a</math>.<br /> | Wenn eine Zahl <math>9</math> ein Teiler von <math>a</math> ist, dann ist <math>3</math> auch ein Teiler von <math>a</math>.<br /> | ||
Voraussetzung: <math>9 \mid a</math><br /> | Voraussetzung: <math>9 \mid a</math><br /> | ||
Version vom 28. April 2018, 13:20 Uhr
AllgemeinWir betrachten die Implikation BeispieleBeispiel 1 TeilbarkeitImplikation: Aus der Teilbarkeit durch 9 folgt die Teilbarkeit durch 3Wenn eine Zahl Unter der Voraussetzung, dass eine ganze Zahl
|
.
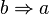ist die Umkehrung der Implikation 
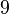ein Teiler von 
ist, dann ist 
auch ein Teiler von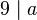 
.
.
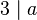
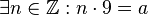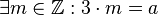existiert, die mit 
gibt, die mit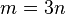 
leistet das Verlangte:
.
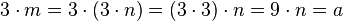