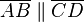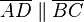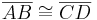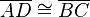Umkehrung von Implikationen SoSe 2018: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Implikation) |
*m.g.* (Diskussion | Beiträge) (→Implikation) |
||
| Zeile 47: | Zeile 47: | ||
::B<sub>1</sub>: <math>\overline{AB} \cong \overline{CD}</math><br /> | ::B<sub>1</sub>: <math>\overline{AB} \cong \overline{CD}</math><br /> | ||
::B<sub>2</sub>: <math>\overline{AD} \cong \overline{BC}</math><br /> | ::B<sub>2</sub>: <math>\overline{AD} \cong \overline{BC}</math><br /> | ||
| + | ===Umkehrung=== | ||
| + | Versuchen Sie sich selbst ...<br /> | ||
| + | Kopieren Sie den Text zur Implikation hier her und ändern Sie ihn einfach entsprechend der Umkehrung ab. Das ist nicht schwer, Sie brauchen mich nicht dafür. Viele Erfolg! --[[Benutzer:*m.g.*|*m.g.*]] ([[Benutzer Diskussion:*m.g.*|Diskussion]]) 19:55, 29. Apr. 2018 (CEST) | ||
==Beispiel 3: Jauch reloaded== | ==Beispiel 3: Jauch reloaded== | ||
Version vom 29. April 2018, 18:55 Uhr
AllgemeinWir betrachten die Implikation BeispieleBeispiel 1: Teilbarkeit durch 3 und 9Implikation: Aus der Teilbarkeit durch 9 folgt die Teilbarkeit durch 3Wenn eine Zahl Unter der Voraussetzung, dass eine ganze Zahl Umkehrung: Aus der Teilbarkeit durch 3 folgt die Teilbarkeit durch 9Wenn eine Zahl durch Beispiel 2: In jedem Parallelogramm sind die gegenüberliegenden Seiten jeweils kongruent zueinanderDer Begriff Parallelogramm sei entsprechend der Semantik der Begriffsbezeichnung definiert:
Implikation
Wir spezifizieren die Aussagen der Implikation bzgl. eines Vierecks
Behauptung:
Wir formulieren Voraussetzung und Behauptung entsprechend der Eckpunktsbezeichnungen unseres Parallelogramms und wenden dabei die Definition des Begriffs Parallelogramm an:
Behauptung für
UmkehrungVersuchen Sie sich selbst ... Beispiel 3: Jauch reloadedImplikation: Jedes Rechteck ist ein ParallelogrammUnter einem Rechteck wollen wir ein Viereck verstehen, dessen Diagonalen kongruent zueinander sind und die sich gegenseitig halbieren.
Voraussetzung
|
 .
.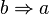 ist die Umkehrung der Implikation
ist die Umkehrung der Implikation 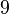 ein Teiler von
ein Teiler von  ist, dann ist
ist, dann ist  auch ein Teiler von
auch ein Teiler von 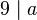
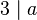
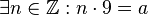 .
.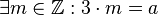 .
. existiert, die mit
existiert, die mit  gibt, die mit
gibt, die mit 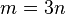 leistet das Verlangte:
leistet das Verlangte: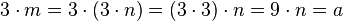 .
.
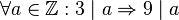
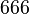 (
(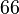 zwar durch
zwar durch  .
.