Übungsaufgaben zur Algebra, Serie 2 SoSe 2018: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Aufgabe 2.1) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 2.1) |
||
| Zeile 5: | Zeile 5: | ||
Gegeben sei <math>DD_\Delta:=\left [ \left \{ \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ \end{pmatrix}, \begin{pmatrix} -\frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} \sqrt{3} & -\frac{1}{2} \sqrt{3} \\ \end{pmatrix}, \begin{pmatrix} a & b \\ c & d \end{pmatrix} \right \}, \circ \right ]</math>. <br /> <math>~</math> <br /> | Gegeben sei <math>DD_\Delta:=\left [ \left \{ \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ \end{pmatrix}, \begin{pmatrix} -\frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} \sqrt{3} & -\frac{1}{2} \sqrt{3} \\ \end{pmatrix}, \begin{pmatrix} a & b \\ c & d \end{pmatrix} \right \}, \circ \right ]</math>. <br /> <math>~</math> <br /> | ||
| − | Bestimmen Sie <math>a, b, c, d \in \mathbb{R}</math> derart, dass <math>DD_\Delta</math> eine Gruppe ist. Die Operation <math>\circ</math> ist dabei als die normale Matrizenmultiplikation zu verstehen. | + | Bestimmen Sie <math>a, b, c, d \in \mathbb{R}</math> derart, dass <math>DD_\Delta</math> eine Gruppe ist. Die Operation <math>\circ</math> ist dabei als die normale Matrizenmultiplikation zu verstehen.<br /> |
| + | <br /> | ||
| + | Hilfe: Öffnen Sie Geogebra. Sie können in Geogebra Matrizen eingeben. Die Matrix <math>M=\begin{pmatrix} -\frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} \sqrt{3} & -\frac{1}{2} \sqrt{3} \\ \end{pmatrix}</math> geben Sie z.B. wie folgt ein:<br /> | ||
| + | <math>M= \left \{ \left \{ -\frac{1}{2} , -\frac{1}{2} \right \} , \left \{ \frac{1}{2} \sqrt{3} , -\frac{1}{2} \sqrt{3} \right \} \right \} </math> | ||
=Aufgabe 2.2= | =Aufgabe 2.2= | ||
Version vom 1. Mai 2018, 15:54 Uhr
Aufgabe 2.1Gegeben sei Bestimmen Sie Aufgabe 2.2 |
![DD_\Delta:=\left [ \left \{ \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ \end{pmatrix}, \begin{pmatrix} -\frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} \sqrt{3} & -\frac{1}{2} \sqrt{3} \\ \end{pmatrix}, \begin{pmatrix} a & b \\ c & d \end{pmatrix} \right \}, \circ \right ]](/images/math/5/f/2/5f20e500bcab3995ec3dca6e5a97b976.png) .
. 
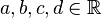 derart, dass
derart, dass 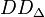 eine Gruppe ist. Die Operation
eine Gruppe ist. Die Operation  ist dabei als die normale Matrizenmultiplikation zu verstehen.
ist dabei als die normale Matrizenmultiplikation zu verstehen.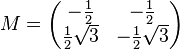 geben Sie z.B. wie folgt ein:
geben Sie z.B. wie folgt ein: