Übungsaufgaben zur Algebra, Serie 2 SoSe 2018: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Aufgabe 2.3)
Zeile 19: Zeile 19:
 
Beweisen Sie <math>a</math> muss das Inverse von <math>b</math> und <math>b</math> muss das Inverse von <math>a</math> sein.<br />
 
Beweisen Sie <math>a</math> muss das Inverse von <math>b</math> und <math>b</math> muss das Inverse von <math>a</math> sein.<br />
 
Was haben Sie mit diesem Beweis gleichzeitig bewiesen?
 
Was haben Sie mit diesem Beweis gleichzeitig bewiesen?
−
 
+
=Aufgabe 2.4=
 +
Beweisen Sie: Bis auf Strukturgleicheit gibt es zwei und nur zwei verschiedene vierelementige Gruppen.
 
<!--- Was hier drunter steht muss stehen bleiben --->
 
<!--- Was hier drunter steht muss stehen bleiben --->
 
|}
 
|}
 
</div>
 
</div>
 
[[Kategorie:Algebra]]
 
[[Kategorie:Algebra]]

Version vom 1. Mai 2018, 15:09 Uhr

Inhaltsverzeichnis

Aufgabe 2.1

Gegeben sei DD_\Delta:=\left [ \left \{ \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ \end{pmatrix}, \begin{pmatrix} -\frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} \sqrt{3} & -\frac{1}{2} \sqrt{3} \\ \end{pmatrix}, \begin{pmatrix} a & b \\ c & d \end{pmatrix} \right \}, \circ \right ].
~

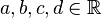Bestimmen Sie a, b, c, d \in \mathbb{R} derart, dass 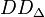DD_\Delta eine Gruppe ist. Die Operation \circ ist dabei als die normale Matrizenmultiplikation zu verstehen.

Hilfe: Öffnen Sie Geogebra. Sie können in Geogebra Matrizen eingeben. Die Matrix
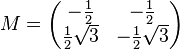
M=\begin{pmatrix} -\frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} \sqrt{3} & -\frac{1}{2} \sqrt{3} \\ \end{pmatrix}
geben Sie z.B. wie folgt ein:
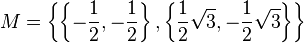M= \left \{ \left \{ -\frac{1}{2} , -\frac{1}{2} \right \} , \left \{ \frac{1}{2} \sqrt{3} , -\frac{1}{2} \sqrt{3} \right \} \right \}.
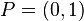Geben Sie jetzt die Koordinaten eines beliebigen Punktes wie etwa P=(0,1) ein. Lassen Sie nun 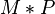M * P berechnen. Es wird eine Bildpunkt von P berechnet ... .

Aufgabe 2.2

Bestimmen Sie die Verknüpfungstafel der Gruppe \left [ \mathbb{Z}_3, \oplus \right ]. (Restklassen modulo 3, mit Restklassenadddition). Vergleichen Sie mit der Gruppentafel aus Aufgabe 2.1.

Aufgabe 2.3

Es sei \left [ \left \{ e, a, b \right \}, \circ \right ] eine Gruppe mit dem Einselement e.
Beweisen Sie a muss das Inverse von b und b muss das Inverse von a sein.
Was haben Sie mit diesem Beweis gleichzeitig bewiesen?

Aufgabe 2.4

Beweisen Sie: Bis auf Strukturgleicheit gibt es zwei und nur zwei verschiedene vierelementige Gruppen.

Von „http://geometrie.zum.de/index.php?title=Übungsaufgaben_zur_Algebra,_Serie_2_SoSe_2018&oldid=31218“