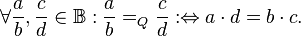Übungsaufgaben zur Algebra, Serie 3 SoSe 2018: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Aufgabe 3.1) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 3.2) |
||
| Zeile 7: | Zeile 7: | ||
=Aufgabe 3.2= | =Aufgabe 3.2= | ||
| + | Auf der Menge aller Brüche <math>\mathbb{B}</math>definieren wir deine Relation Quotientengleich <math>=_Q</math>: <br /> | ||
| + | <math>\forall \frac{a}{b}, \frac{c}{d} \in \mathbb{B}: \frac{a}{b} =_Q \frac{c}{d} :\Leftrightarrow a \cdot d = b \cdot c.</math><br /> | ||
| + | |||
=Aufgabe 3.3= | =Aufgabe 3.3= | ||
=Aufgabe 3.4= | =Aufgabe 3.4= | ||
Version vom 5. Mai 2018, 14:53 Uhr
Aufgabe 3.1Es seien Aufgabe 3.2Auf der Menge aller Brüche Aufgabe 3.3Aufgabe 3.4Aufgabe 3.5Aufgabe 3.6Aufgabe 3.7Aufgabe 3.8Aufgabe 3.9Aufgabe 3.10 |
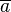und 
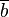zwei Restklassen bzgl. des selben Moduls 
. Beweisen Sie die Repräsentantenunabhängigkeit Restklassenaddition: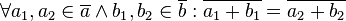
.
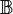definieren wir deine Relation Quotientengleich 
: 
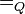