Serie 4: größere LSG lösen SoSe 2018: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „<div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#B9D0F0; align:left;"> {|width=90%| style="backgro…“) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 4.1 SoSe 2018) |
||
| Zeile 5: | Zeile 5: | ||
=Aufgabe 4.1 SoSe 2018= | =Aufgabe 4.1 SoSe 2018= | ||
| + | Es seien <math>\varepsilon_x, \varepsilon_y, \varepsilon_z</math> drei Ebenen im <math>\mathbb{R}^3</math>, die genau den Punkt <math>S=(\pi,e,\sqrt{2})</math> gemeinsam haben.<br /> Ferner gelte:<br /> | ||
| + | |||
| + | *<math>\varepsilon_x</math> ist parallel zur <math>y-z-</math>Ebene, | ||
| + | *<math>\varepsilon_y</math> ist parallel zur <math>x-z-</math>Ebene, | ||
| + | *<math>\varepsilon_z</math> ist parallel zur <math>x-y-</math>Ebene. | ||
| + | |||
| + | <br /> | ||
| + | Beschreiben Sie die drei Ebenen <math>\varepsilon_x, \varepsilon_y, \varepsilon_z </math> mittels Gleichungen vom Typ <math>ax+by+cz=d</math>. | ||
=Aufgabe 4.2 SoSe 2018= | =Aufgabe 4.2 SoSe 2018= | ||
Version vom 13. Mai 2018, 11:57 Uhr
Aufgabe 4.1 SoSe 2018Es seien
Aufgabe 4.2 SoSe 2018Aufgabe 4.3 SoSe 2018Aufgabe 4.5 SoSe 2018Aufgabe 4.6 SoSe 2018Aufgabe 4.7 SoSe 2018Aufgabe 4.8 SoSe 2018Aufgabe 4.9 SoSe 2018Aufgabe 4.10 SoSe 2018 |
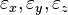 drei Ebenen im
drei Ebenen im 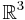 , die genau den Punkt
, die genau den Punkt 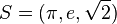 gemeinsam haben.
gemeinsam haben.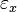 ist parallel zur
ist parallel zur 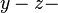 Ebene,
Ebene,
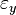 ist parallel zur
ist parallel zur 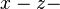 Ebene,
Ebene,
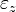 ist parallel zur
ist parallel zur 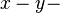 Ebene.
Ebene.
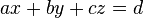 .
.

