Serie 4: größere LSG lösen SoSe 2018: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Aufgabe 4.1 SoSe 2018) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 4.2 SoSe 2018) |
||
| Zeile 15: | Zeile 15: | ||
=Aufgabe 4.2 SoSe 2018= | =Aufgabe 4.2 SoSe 2018= | ||
| + | Geben Sie ein lineares Gleichungssystem vom Typ <br /> | ||
| + | <math>\begin{matrix} | ||
| + | a_{11}x &+& a_{12}y &+& a_{13}z &=& b_1 \\ | ||
| + | a_{21}x &+& a_{22}y &+& a_{23}z &=& b_2 \\ | ||
| + | a_{31}x &+& a_{32}y &+& a_{33}z &=& b_3 | ||
| + | \end{matrix} | ||
| + | </math><br /> | ||
| + | an, bei dem keiner der Koeffizienten Null ist und das die Lösungsmenge <math>L=\{(\pi,e,\sqrt{2})\}</math> hat. | ||
=Aufgabe 4.3 SoSe 2018= | =Aufgabe 4.3 SoSe 2018= | ||
Version vom 13. Mai 2018, 12:09 Uhr
Aufgabe 4.1 SoSe 2018Es seien
Aufgabe 4.2 SoSe 2018Geben Sie ein lineares Gleichungssystem vom Typ Aufgabe 4.3 SoSe 2018Aufgabe 4.5 SoSe 2018Aufgabe 4.6 SoSe 2018Aufgabe 4.7 SoSe 2018Aufgabe 4.8 SoSe 2018Aufgabe 4.9 SoSe 2018Aufgabe 4.10 SoSe 2018 |
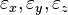 drei Ebenen im
drei Ebenen im 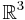 , die genau den Punkt
, die genau den Punkt 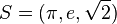 gemeinsam haben.
gemeinsam haben.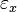 ist parallel zur
ist parallel zur 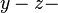 Ebene,
Ebene,
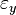 ist parallel zur
ist parallel zur 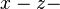 Ebene,
Ebene,
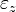 ist parallel zur
ist parallel zur 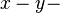 Ebene.
Ebene.
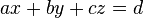 .
.
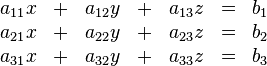
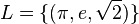 hat.
hat.

