SoSe 2018 Lösung von Aufgabe 6.01: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Beweis 1) |
*m.g.* (Diskussion | Beiträge) (→Der Beweis) |
||
| Zeile 41: | Zeile 41: | ||
Wenn Fall 1 eintritt folgt Fall a.<br /> | Wenn Fall 1 eintritt folgt Fall a.<br /> | ||
Es bleibt zu zeigen: <br /> | Es bleibt zu zeigen: <br /> | ||
| − | <math>P \in AB \land \vert AP\vert > \vert BP\vert \Rightarrow \operatorname{Zw}(A,B,P) </math> | + | <math>P \in AB \land \vert AP\vert > \vert BP\vert \Rightarrow \operatorname{Zw}(A,B,P) </math><br /> |
| + | Ferner dürfen wir für diesen Beweis voraussetzen, dass <math>P \not \in \overline{AB}</math>, denn Fall 1 wurde schon abgearbeitet.<br /> | ||
| + | Von drei paarweise verschiedenen Punkten <math>A, B, P</math> liegt genau einer zwischen den beiden anderen (in der Vorlesung bewiesen).<br /> | ||
| + | Prinzipiell könnte also gelten:<br /> | ||
| + | <math> | ||
| + | |||
| + | \begin{matrix} | ||
| + | \text{I} & \operatorname{Zw}(APB) \\ | ||
| + | \text{II} & \operatorname{Zw}(PAB) \\ | ||
| + | \text{III} & \operatorname{Zw}(ABP) \\ | ||
| + | \end{matrix} | ||
| + | |||
| + | </math> | ||
| + | |||
Version vom 10. Juni 2018, 15:55 Uhr
Aufgabe 6.01In einer Übung definierte eine Kommilitonin den Begriff Halbgerade
Lösung 1Behauptung: Def V <=> Def Ü zz. P Element von AB, d.h. P muss zwischen den Punkten A und B liegen Strecke AB ist größer als Strecke AP Kommentar --*m.g.* (Diskussion) 16:32, 10. Jun. 2018 (CEST)Hier ist Luft nach oben. Natürlich können wir beide Implikationen zusammenfassen zu einer Äquivalenz. Def Ü genau dann, wenn Def V. Dazu sind zwei Beweise zu führen. Beweis 1Wenn VoraussetzungIn diesem Fall gilt: Anders ausgedrückt: Fall 1
Fall 2
Behauptung
Fall a
Fall b
Der BeweisWenn Fall 1 eintritt folgt Fall a.
|
 wie folgt:
wie folgt: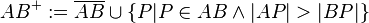
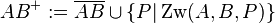 Beweisen Sie:
Beweisen Sie:
 Definition Ü
Definition Ü
 ein Punkt des Strahls
ein Punkt des Strahls  oder es gilt
oder es gilt 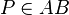 und
und 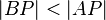 .
.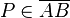
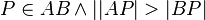
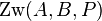
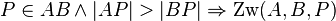
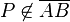 , denn Fall 1 wurde schon abgearbeitet.
, denn Fall 1 wurde schon abgearbeitet.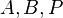 liegt genau einer zwischen den beiden anderen (in der Vorlesung bewiesen).
liegt genau einer zwischen den beiden anderen (in der Vorlesung bewiesen).