Restklassen modulo 4 mit der Restklassenmultiplikation: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Wir überprüfen ob <math>[R</math><sub>4</sub><math>,\odot ]</math> eine Gruppe ist. Hierfür betrachten wir die Verknüpfungstafel: <table> <tr> <th><math>…“) |
K |
||
| Zeile 16: | Zeile 16: | ||
<h2>Assoziativität</h2> | <h2>Assoziativität</h2> | ||
| − | <span style="color:green;">Passt</span>, denn die Restklassenmultiplikation ist definiert durch <math>\overline{a},\overline{b}\isin R</math><sub>4</sub><math>, \overline{a} \odot \overline{b} := \overline{a \sdot b}</math> | + | <span style="color:green;">Passt</span>, denn die Restklassenmultiplikation ist definiert durch <math>\overline{a},\overline{b}\isin R</math><sub>4</sub><math>, \overline{a} \odot \overline{b} := \overline{a \sdot b}</math> mit <math>a,b \isin \Z </math> |
Somit lässt sich <math>(\overline{a} \odot \overline{b} )\odot \overline{c} = \overline{a} \odot (\overline{b} \odot \overline{c} )</math> | Somit lässt sich <math>(\overline{a} \odot \overline{b} )\odot \overline{c} = \overline{a} \odot (\overline{b} \odot \overline{c} )</math> | ||
| Zeile 22: | Zeile 22: | ||
auch so schreiben: <math>(\overline{a \sdot b )\sdot c} = \overline{a \sdot (b \sdot c} )</math> mit <math>a,b,c \isin \Z </math> | auch so schreiben: <math>(\overline{a \sdot b )\sdot c} = \overline{a \sdot (b \sdot c} )</math> mit <math>a,b,c \isin \Z </math> | ||
| − | und die Assoziativität in <math>\Z</math> | + | und die Assoziativität in <math>\Z</math> gilt als bewiesen. |
<h2>neutrales Element</h2> | <h2>neutrales Element</h2> | ||
Aktuelle Version vom 11. Juli 2018, 15:44 Uhr
Wir überprüfen ob 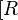 4
4![,\odot ]](/images/math/7/9/3/79395ee9e32eb5bc2cf78d55193a1ba4.png) eine Gruppe ist. Hierfür betrachten wir die Verknüpfungstafel:
eine Gruppe ist. Hierfür betrachten wir die Verknüpfungstafel:
 |  |  |  |  |
|---|---|---|---|---|
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  | 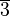 |  |  |
Inhaltsverzeichnis |
Abgeschlossenheit
Passt, weil wir sehen können, dass jeder Eintrag, also jedes Ergebnis einer Restklassenmultiplikation, ebenfalls in derselben Restklasse ist.
Assoziativität
Passt, denn die Restklassenmultiplikation ist definiert durch 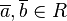 4
4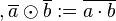 mit
mit 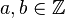
Somit lässt sich 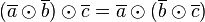
auch so schreiben: 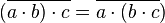 mit
mit 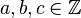
und die Assoziativität in 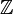 gilt als bewiesen.
gilt als bewiesen.
neutrales Element
Passt, denn anhand der Verknüpfungstafel ist zu sehen, dass die  das neutrale Element von
das neutrale Element von 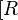 4
4![,\odot ]](/images/math/7/9/3/79395ee9e32eb5bc2cf78d55193a1ba4.png) ist.
ist.
inverses Element
Passt nicht! In der Verknüpfungstafel sehen wir, das die  und die
und die 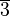 zwar ein inverses Element haben, die
zwar ein inverses Element haben, die  allerdings nicht.
allerdings nicht.
Resultat
Somit ist 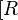 4
4![,\odot ]](/images/math/7/9/3/79395ee9e32eb5bc2cf78d55193a1ba4.png) keine Gruppe.
keine Gruppe.

