Lösung von Aufgabe 5.3 P (WS 18 19): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
Zeile 2: Zeile 2:
  
 
<math>M</math>  <math>\epsilon</math>  <math>D</math> = <math>\big\{Q,R\big\}</math>  --Pippilotta Viktualia Rollgardina Pfefferminz Efraimstochter Langstrumpf 18:57, 15. Nov. 2018 (CET)
 
<math>M</math>  <math>\epsilon</math>  <math>D</math> = <math>\big\{Q,R\big\}</math>  --Pippilotta Viktualia Rollgardina Pfefferminz Efraimstochter Langstrumpf 18:57, 15. Nov. 2018 (CET)
 +
 +
M={Drachen, Raute, Quadrat} --[[Benutzer:CIG UA|CIG UA]] ([[Benutzer Diskussion:CIG UA|Diskussion]]) 20:11, 18. Nov. 2018 (CET)
  
  

Version vom 18. November 2018, 20:11 Uhr

a) Geben Sie die Menge M aller konvexer Drachenvierecke an.

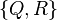M \epsilon D = \big\{Q,R\big\} --Pippilotta Viktualia Rollgardina Pfefferminz Efraimstochter Langstrumpf 18:57, 15. Nov. 2018 (CET)

M={Drachen, Raute, Quadrat} --CIG UA (Diskussion) 20:11, 18. Nov. 2018 (CET)


b) Bilden Sie das kartesische Produkt der Menge M \times M.

D R Q
D (D,D) (D,R) (D,Q)
R (R,D) (R,R) (R,Q)
Q (Q,D) (Q,R) (Q,Q) 


M \times M
 = \big\{ (D,D); (D,R); (D,Q); (R,D); (R,R); (R,Q); (Q,D); (Q,R); (Q,Q)\big\}--Pippilotta Viktualia Rollgardina Pfefferminz Efraimstochter Langstrumpf 18:57, 15. Nov. 2018 (CET)


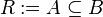c) Wir definineren eine Relation R mit R:=A\subseteq B. Bestimmen Sie die Relation R auf M \times M.


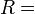
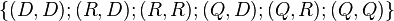R= \big\{ (D,D); (R,D); (R,R); (Q,D); (Q,R); (Q,Q)\big\}--Pippilotta Viktualia Rollgardina Pfefferminz Efraimstochter Langstrumpf 18:58, 15. Nov. 2018 (CET)


d) Untersuchen Sie die Relation R auf ihre Eigenschaften (reflexiv, symmetrisch, transitiv).

reflexiv Ja denn: (Q,Q); (R,R); (D,D)

nicht symmetrisch denn: (Q,D) ==> (D,Q) Stimmt nicht.

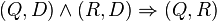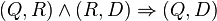transitiv Ja denn: (Q,D) \wedge (R,D) \Rightarrow (Q,R) und (Q,R) \wedge (R,D) \Rightarrow (Q,D) --Pippilotta Viktualia Rollgardina Pfefferminz Efraimstochter Langstrumpf 19:05, 15. Nov. 2018 (CET)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_5.3_P_(WS_18_19)&oldid=32500“