Lösung von Zusatzaufg.7.3P (WS 18 19): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Beweisen Sie: Das Innere eines Dreiecks ist konvex.<br /> Kategorie:Geo_P“) |
CIG UA (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
Beweisen Sie: Das Innere eines Dreiecks ist konvex.<br /> | Beweisen Sie: Das Innere eines Dreiecks ist konvex.<br /> | ||
| + | |||
| + | Das Innere eines Dreiecks ist die Schnittmenge von 3 Halbebenen: <math>\overline{ABC}</math> = <math>\overline{AB}C^+</math> <span>∩</span> <math>\overline{AC}B^+</math> <span>∩</span> <math>\overline{BC}A^+</math><br /> | ||
| + | => Halbebenen sind konvexe Mengen. <br /> | ||
| + | => Das Innere eines Dreiecks ist eine Schnittmenge konvexer Mengen<br /> | ||
| + | => Das Innere eines Dreiecks ist eine konvexe Menge. --[[Benutzer:CIG UA|CIG UA]] ([[Benutzer Diskussion:CIG UA|Diskussion]]) 15:38, 30. Nov. 2018 (CET) | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Version vom 30. November 2018, 15:38 Uhr
Beweisen Sie: Das Innere eines Dreiecks ist konvex.
Das Innere eines Dreiecks ist die Schnittmenge von 3 Halbebenen:  =
= 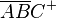 ∩
∩ 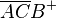 ∩
∩ 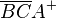
=> Halbebenen sind konvexe Mengen.
=> Das Innere eines Dreiecks ist eine Schnittmenge konvexer Mengen
=> Das Innere eines Dreiecks ist eine konvexe Menge. --CIG UA (Diskussion) 15:38, 30. Nov. 2018 (CET)

