Lösung von Aufgabe 9.1P (WS 18/19): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Beweisen Sie die Halbgeradentreue der Geradenspiegelung. Nutzen Sie für den Beweis die Streckentreue der Geradenspiegelung und eine geeignete Definition des B…“) |
CIG UA (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
Beweisen Sie die Halbgeradentreue der Geradenspiegelung. Nutzen Sie für den Beweis die Streckentreue der Geradenspiegelung und eine geeignete Definition des Begriffs Halbgerade. | Beweisen Sie die Halbgeradentreue der Geradenspiegelung. Nutzen Sie für den Beweis die Streckentreue der Geradenspiegelung und eine geeignete Definition des Begriffs Halbgerade. | ||
<br /> | <br /> | ||
| + | |||
| + | Vor: S<sub>g</sub>(<math>AB^+</math>) Beh: =<math>A'B'^+</math><br /> | ||
| + | 1.) <math>AB^+</math> = <math>\overline{AB}</math> vereinigt mit {P|Zw(A,B,P)} '''- Vor., Def Halbgerade'''<br /> | ||
| + | 2.) B ε <math>\overline{AP}</math> '''- 1.)'''<br /> | ||
| + | |||
| + | 3.) S<sub>g</sub>(<math>\overline{AP}</math>) = <math>\overline{A'P'}</math> <math>\wedge</math> S<sub>g</sub>(<math>\overline{AB}</math>) = S<sub>g</sub>(<math>\overline{A'B'}</math>) mit |AP| = |A'P'| und |AB| = |A'B'| '''- Streckentreue'''<br /> | ||
| + | 4.) B' ε <math>\overline{A'P'}</math> '''- 2.), 3.)''' <br /> | ||
| + | 5.) Zw (A',B',P') '''- 4.), Zwischenrelation''' <br /> | ||
| + | 6.) <math>A'B'^+</math> = <math>A'B'</math> vereinigt mit {P'|Zw(A',B',P')} '''- 5.), Def Halbgerade'''<br /> | ||
| + | => S<sub>g</sub>(<math>AB^+</math>) = <math>A'B'^+</math><br /> | ||
| + | --[[Benutzer:CIG UA|CIG UA]] ([[Benutzer Diskussion:CIG UA|Diskussion]]) 11:36, 14. Dez. 2018 (CET) | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Version vom 14. Dezember 2018, 11:36 Uhr
Beweisen Sie die Halbgeradentreue der Geradenspiegelung. Nutzen Sie für den Beweis die Streckentreue der Geradenspiegelung und eine geeignete Definition des Begriffs Halbgerade.
Vor: Sg( ) Beh: =
) Beh: =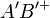
1.)  =
=  vereinigt mit {P|Zw(A,B,P)} - Vor., Def Halbgerade
vereinigt mit {P|Zw(A,B,P)} - Vor., Def Halbgerade
2.) B ε 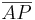 - 1.)
- 1.)
3.) Sg(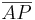 ) =
) = 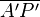
 Sg(
Sg( ) = Sg(
) = Sg(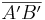 ) mit |AP| = |A'P'| und |AB| = |A'B'| - Streckentreue
) mit |AP| = |A'P'| und |AB| = |A'B'| - Streckentreue
4.) B' ε 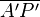 - 2.), 3.)
- 2.), 3.)
5.) Zw (A',B',P') - 4.), Zwischenrelation
6.) 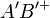 =
= 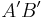 vereinigt mit {P'|Zw(A',B',P')} - 5.), Def Halbgerade
vereinigt mit {P'|Zw(A',B',P')} - 5.), Def Halbgerade
=> Sg( ) =
) = 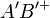
--CIG UA (Diskussion) 11:36, 14. Dez. 2018 (CET)

