Lösung von Aufgabe 10.4P (WS 18/19): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
CIG UA (Diskussion | Beiträge) |
|||
| Zeile 1: | Zeile 1: | ||
Beweisen Sie: Bei Spiegelungen, Stöße beim Billard über Bande, etc. gilt stets: Einfallswinkel <math>\alpha</math> gleich Ausfallswinkel <math>\beta</math> (siehe GeoGebra-Applet).<br /> <br />Falls nichts angezeigt wird, können Sie mit folgendem Link [{{fullurl:{{PAGENAME}}|action=purge}} den Servercache leeren] | Beweisen Sie: Bei Spiegelungen, Stöße beim Billard über Bande, etc. gilt stets: Einfallswinkel <math>\alpha</math> gleich Ausfallswinkel <math>\beta</math> (siehe GeoGebra-Applet).<br /> <br />Falls nichts angezeigt wird, können Sie mit folgendem Link [{{fullurl:{{PAGENAME}}|action=purge}} den Servercache leeren] | ||
<ggb_applet width="536" height="428" version="4.0" ggbBase64="UEsDBBQACAAIAAli4UAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAAli4UAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s5VnNcts2ED6nT4HhoadIAgiQlFIpmcRxp55x2k6ddjq9gSQsoaYIloB+nOlLNQ+SZ+oCIClKcpzacdJ06rEMgFjsYr/9dgHK02fbZYHWotZSlbOADHGARJmpXJbzWbAyl4Nx8OzpV9O5UHOR1hxdqnrJzSxgVlLmsyDjnI3zkA0IZnjABBUDLrAYECYYTyaURWkeILTV8kmpvudLoSueiYtsIZb8XGXcOMMLY6ono9Fmsxm2poaqno/m83S41aAAtlnqWdB0noC6vUUb6sRDjMno11fnXv1AltrwMhMBsi6s5NOvHk03sszVBm1kbhazIGIsQAsh5wvr0wR8GlmhCgCpRGbkWmhY2hs6n82yCpwYL+38I99DRedOgHK5lrmoZwEe0jiJWYKj8TikUTixFlUtRWkaYdIYHbXqpmspNl6v7TmTsMgoVaTcqkR//olCHGL02DbENyE0ceynsH+GqW9C3zDfRF6G+eXMizIvw7wMowFaSy3TQsyCS15ogFCWlzWErxtrc10It5/mwc598hh80vINCFMMmHrM4TnGj+0nhg/DDdg9J0nPqqlXdzTamoxo/M9Nhh/lKG1thje5GUbvcTO+xaj3+5/4SaKeTTDlft3nyCK9zc1Di378cQZj9llcnI7aVJk22YH0wso27DFiqW2+0AmKJpb2BEWQG3ECLI8QmUCThAiyAZEIsQiGZIxi2yaIJjDBEEVjZOUIRS45ojH8YYlTFqMIlNmnCeQkImCIoYgi4nKKIcgk5PIScjSkIBFFKIJF1jwJrQoaIxbDiI4Rgz3alEwICFJYCGMwHyJKELWLSYLCGMVWH2E21eOx3TqoDFGMUUysQshqyGifzSA/RtR6EzdwybJamT2IsmXedo2quliANNSjXdnz9WmvKj6aFjwVBRwUFzaSCK15YTPCGbpUpUFtEEP/bF7zaiEzfSGMgVUa/c7X/Jwbsf0WpHVr28lmqtQ/1sqcqGK1LDVCmSpwt2dVkF4/7HYNA9qbYP2JqDcR9/rJjXYVzKCVFmBf1boV53l+ZiV2pQGQ/KEsrl/Ugl9VSu67MR25M2cqVlkhc8nLX4Cs1orFBXVHkC1X7RFEw6TdiKrzi2sNDEbb30StoMYQNpz0f5IAXfspSqIh7v+ASp1xm3xssr9oDFPXzVyE91c1wRPrLkR8K3bezmvZkcX2z/QLVeTdtPP/hFdmVbvbAxTH2nr1vJwXwnHElVs4mrOrVG0vPDmo1/X6uoIR9htI5w53BLUhjCIQaNrUt07G7qyTwk4GOwncsk3m3TyZhE7CtalvnRTQ12+t8ZS0XhLcmpHaVTQcNHnTVitLfnvSr0ppztuBkdlV4yrxC75fLVPRUWhfJ3kondPRAcemV6IuRdFQGmK5UivtM7TH9lxkcglDP9FAwm24foYN+Ke5mNei3XjhbmYeMDeL+2w9euxUfVur5Vm5fg1cONjAdNTucqqzWlaWciiFY+BK7FiVS83hFMn762wOguuZPS0AHmOhgexcmYWq3eULigq0NvUKsYSbFjKOXo6hHczP3R3O4olU+jvUte7o8/O7gMH0jVRzpORFteD2ntc4XfBrUe/B4PS9UvkhOIC98wCSvLIKbHQrITwx/I6hU4FCl097ZQrw1mg7CwahvYhfQ7bZ9o2/wvs7rHXWJtleYfZPDyIF9PE4fQCxF18WYvfBK3pguDK1XPIyR6W72ZxDOQl2By3HlmWIEwudx2Vl2gnuVTUKjpC3lakDln8A+J6r70Me3x/3HXq4QS9p0BuEHX67SmrgkL+CNxntyr1pCrvrfCfzXLgLnj9o/ij9Eu3Lm1xWhcykuQsnT/77nOxyGH8SUr6Sda3qA1qeeFryI1qefM0rpb+5nZwHIWiW/KuBuAHO+DOUxJf/ffrRIRs7vMiQsM9TFFvGOA6+POJgeofSmH4hpZEN3c3anjAWTlcc6RBe9T95ddxH+6w0cDUEHA4g5x7s9Ajs07uk+um96G6/DZj7JvXNA+ANZxDtv9h4CmNI/tjBT9kQhw9I4wsxt89vrqOnR7Bmt8OqG20tcNkXQuMB7S5IdBwmJMZs4jue0/GnOu8deIUtUx2Doawdv7NcCVHZl8Ufytc1L7X9PtrL9N6F3hNB9yJ68/XsFJrQRvMwjO/+uj2O7hWnixJIu+9vebFqAR4mUODxOIoYJROW4AaK+50YBB+Hmtwt1PeJG6+zXva0R09RqM1P4rIQWwfsx0Th5V4Uju/K797eKQpvPxCFGKrF/y4Ko/5bs/tyqvlHy9O/AVBLBwhsZZadrAYAAAUaAABQSwECFAAUAAgACAAJYuFA1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAAli4UBsZZadrAYAAAUaAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAQwcAAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /><br /> | <ggb_applet width="536" height="428" version="4.0" ggbBase64="UEsDBBQACAAIAAli4UAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAAli4UAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s5VnNcts2ED6nT4HhoadIAgiQlFIpmcRxp55x2k6ddjq9gSQsoaYIloB+nOlLNQ+SZ+oCIClKcpzacdJ06rEMgFjsYr/9dgHK02fbZYHWotZSlbOADHGARJmpXJbzWbAyl4Nx8OzpV9O5UHOR1hxdqnrJzSxgVlLmsyDjnI3zkA0IZnjABBUDLrAYECYYTyaURWkeILTV8kmpvudLoSueiYtsIZb8XGXcOMMLY6ono9Fmsxm2poaqno/m83S41aAAtlnqWdB0noC6vUUb6sRDjMno11fnXv1AltrwMhMBsi6s5NOvHk03sszVBm1kbhazIGIsQAsh5wvr0wR8GlmhCgCpRGbkWmhY2hs6n82yCpwYL+38I99DRedOgHK5lrmoZwEe0jiJWYKj8TikUTixFlUtRWkaYdIYHbXqpmspNl6v7TmTsMgoVaTcqkR//olCHGL02DbENyE0ceynsH+GqW9C3zDfRF6G+eXMizIvw7wMowFaSy3TQsyCS15ogFCWlzWErxtrc10It5/mwc598hh80vINCFMMmHrM4TnGj+0nhg/DDdg9J0nPqqlXdzTamoxo/M9Nhh/lKG1thje5GUbvcTO+xaj3+5/4SaKeTTDlft3nyCK9zc1Di378cQZj9llcnI7aVJk22YH0wso27DFiqW2+0AmKJpb2BEWQG3ECLI8QmUCThAiyAZEIsQiGZIxi2yaIJjDBEEVjZOUIRS45ojH8YYlTFqMIlNmnCeQkImCIoYgi4nKKIcgk5PIScjSkIBFFKIJF1jwJrQoaIxbDiI4Rgz3alEwICFJYCGMwHyJKELWLSYLCGMVWH2E21eOx3TqoDFGMUUysQshqyGifzSA/RtR6EzdwybJamT2IsmXedo2quliANNSjXdnz9WmvKj6aFjwVBRwUFzaSCK15YTPCGbpUpUFtEEP/bF7zaiEzfSGMgVUa/c7X/Jwbsf0WpHVr28lmqtQ/1sqcqGK1LDVCmSpwt2dVkF4/7HYNA9qbYP2JqDcR9/rJjXYVzKCVFmBf1boV53l+ZiV2pQGQ/KEsrl/Ugl9VSu67MR25M2cqVlkhc8nLX4Cs1orFBXVHkC1X7RFEw6TdiKrzi2sNDEbb30StoMYQNpz0f5IAXfspSqIh7v+ASp1xm3xssr9oDFPXzVyE91c1wRPrLkR8K3bezmvZkcX2z/QLVeTdtPP/hFdmVbvbAxTH2nr1vJwXwnHElVs4mrOrVG0vPDmo1/X6uoIR9htI5w53BLUhjCIQaNrUt07G7qyTwk4GOwncsk3m3TyZhE7CtalvnRTQ12+t8ZS0XhLcmpHaVTQcNHnTVitLfnvSr0ppztuBkdlV4yrxC75fLVPRUWhfJ3kondPRAcemV6IuRdFQGmK5UivtM7TH9lxkcglDP9FAwm24foYN+Ke5mNei3XjhbmYeMDeL+2w9euxUfVur5Vm5fg1cONjAdNTucqqzWlaWciiFY+BK7FiVS83hFMn762wOguuZPS0AHmOhgexcmYWq3eULigq0NvUKsYSbFjKOXo6hHczP3R3O4olU+jvUte7o8/O7gMH0jVRzpORFteD2ntc4XfBrUe/B4PS9UvkhOIC98wCSvLIKbHQrITwx/I6hU4FCl097ZQrw1mg7CwahvYhfQ7bZ9o2/wvs7rHXWJtleYfZPDyIF9PE4fQCxF18WYvfBK3pguDK1XPIyR6W72ZxDOQl2By3HlmWIEwudx2Vl2gnuVTUKjpC3lakDln8A+J6r70Me3x/3HXq4QS9p0BuEHX67SmrgkL+CNxntyr1pCrvrfCfzXLgLnj9o/ij9Eu3Lm1xWhcykuQsnT/77nOxyGH8SUr6Sda3qA1qeeFryI1qefM0rpb+5nZwHIWiW/KuBuAHO+DOUxJf/ffrRIRs7vMiQsM9TFFvGOA6+POJgeofSmH4hpZEN3c3anjAWTlcc6RBe9T95ddxH+6w0cDUEHA4g5x7s9Ajs07uk+um96G6/DZj7JvXNA+ANZxDtv9h4CmNI/tjBT9kQhw9I4wsxt89vrqOnR7Bmt8OqG20tcNkXQuMB7S5IdBwmJMZs4jue0/GnOu8deIUtUx2Doawdv7NcCVHZl8Ufytc1L7X9PtrL9N6F3hNB9yJ68/XsFJrQRvMwjO/+uj2O7hWnixJIu+9vebFqAR4mUODxOIoYJROW4AaK+50YBB+Hmtwt1PeJG6+zXva0R09RqM1P4rIQWwfsx0Th5V4Uju/K797eKQpvPxCFGKrF/y4Ko/5bs/tyqvlHy9O/AVBLBwhsZZadrAYAAAUaAABQSwECFAAUAAgACAAJYuFA1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAAli4UBsZZadrAYAAAUaAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAQwcAAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /><br /> | ||
| − | + | <br /> | |
| + | <br /> | ||
| + | Vor: <math>\angle CEA </math> = <math>\alpha</math> Beh: <math>\alpha</math> = <math>\beta</math><br /> | ||
| + | 1.) S<sub>AB</sub>(C)= C' => <math>\angle CEA </math> = <math>\angle C'EA </math>. α = α' '''- Vor.'''<br /> | ||
| + | 2.) AB geschnitten C'D = {E} => <math>\angle C'EA </math> = <math>\angle DEB </math> - Def. Scheitelwinkel<br /> | ||
| + | 3.) α' = β '''- 2.)'''<br /> | ||
| + | => α = β. Die Behauptung ist bewiesen.--[[Benutzer:CIG UA|CIG UA]] ([[Benutzer Diskussion:CIG UA|Diskussion]]) 21:56, 20. Dez. 2018 (CET) | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Version vom 20. Dezember 2018, 21:56 Uhr
Beweisen Sie: Bei Spiegelungen, Stöße beim Billard über Bande, etc. gilt stets: Einfallswinkel 
gleich Ausfallswinkel 
(siehe GeoGebra-Applet).
Falls nichts angezeigt wird, können Sie mit folgendem Link den Servercache leeren
Vor: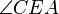 
= Beh: =
1.) SAB(C)= C' => =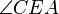 
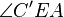. α = α' - Vor.
2.) AB geschnitten C'D = {E} => =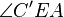 
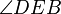- Def. Scheitelwinkel
3.) α' = β - 2.)
=> α = β. Die Behauptung ist bewiesen.--CIG UA (Diskussion) 21:56, 20. Dez. 2018 (CET)
