Lösung von Aufgabe 10.4P (WS 18/19): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
CIG UA (Diskussion | Beiträge) |
CIG UA (Diskussion | Beiträge) |
||
| Zeile 3: | Zeile 3: | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| − | Vor: <math>\angle CEA </math> = <math>\alpha</math> Beh: <math>\alpha</math> = <math>\beta</math><br /> | + | Vor: <math>\angle CEA </math> = <math>\alpha</math> und <math>\angle DEB</math> = <math>\beta</math>; Beh: <math>\alpha</math> = <math>\beta</math><br /> |
1.) S<sub>AB</sub>(C)= C' => <math>\angle CEA </math> = <math>\angle C'EA </math>. α = α' '''- Vor.'''<br /> | 1.) S<sub>AB</sub>(C)= C' => <math>\angle CEA </math> = <math>\angle C'EA </math>. α = α' '''- Vor.'''<br /> | ||
| − | 2.) AB geschnitten C'D = {E} => <math>\angle C'EA </math> = <math>\angle DEB </math> - Def. Scheitelwinkel<br /> | + | 2.) AB geschnitten C'D = {E} => <math>\angle C'EA </math> = <math>\angle DEB </math> '''- Def. Scheitelwinkel'''<br /> |
3.) α' = β '''- 2.)'''<br /> | 3.) α' = β '''- 2.)'''<br /> | ||
=> α = β. Die Behauptung ist bewiesen.--[[Benutzer:CIG UA|CIG UA]] ([[Benutzer Diskussion:CIG UA|Diskussion]]) 21:56, 20. Dez. 2018 (CET) | => α = β. Die Behauptung ist bewiesen.--[[Benutzer:CIG UA|CIG UA]] ([[Benutzer Diskussion:CIG UA|Diskussion]]) 21:56, 20. Dez. 2018 (CET) | ||
Aktuelle Version vom 20. Dezember 2018, 21:57 Uhr
Beweisen Sie: Bei Spiegelungen, Stöße beim Billard über Bande, etc. gilt stets: Einfallswinkel 
gleich Ausfallswinkel 
(siehe GeoGebra-Applet).
Falls nichts angezeigt wird, können Sie mit folgendem Link den Servercache leeren
Vor: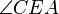 
= und 
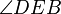= ; Beh: =
1.) SAB(C)= C' => =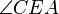 
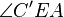. α = α' - Vor.
2.) AB geschnitten C'D = {E} => 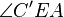= 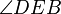- Def. Scheitelwinkel
3.) α' = β - 2.)
=> α = β. Die Behauptung ist bewiesen.--CIG UA (Diskussion) 21:56, 20. Dez. 2018 (CET)
