Lösung von Aufgabe 11.5P (WS 18 19): Unterschied zwischen den Versionen
CIG UA (Diskussion | Beiträge) |
|||
| Zeile 1: | Zeile 1: | ||
#Gegeben sei ein Winkel <math>\angle ABC</math> und ein Punkt ''P'' im Inneren des Winkels der nicht auf einem der Schenkel des Winkels <math>\angle ABC</math> liegt. Konstruieren Sie eine Strecke <math>\overline{DE}</math> deren Endpunkte ''D'' und ''E'' jeweils auf einem der beiden Schenkel des Winkels <math>\angle ABC</math> liegen und ''P'' Mittelpunkt der Strecke <math>\overline{DE}</math> ist. | #Gegeben sei ein Winkel <math>\angle ABC</math> und ein Punkt ''P'' im Inneren des Winkels der nicht auf einem der Schenkel des Winkels <math>\angle ABC</math> liegt. Konstruieren Sie eine Strecke <math>\overline{DE}</math> deren Endpunkte ''D'' und ''E'' jeweils auf einem der beiden Schenkel des Winkels <math>\angle ABC</math> liegen und ''P'' Mittelpunkt der Strecke <math>\overline{DE}</math> ist. | ||
#Beweisen Sie, dass Ihre Konstruktion richtig ist. | #Beweisen Sie, dass Ihre Konstruktion richtig ist. | ||
| − | + | <br /> | |
| + | <br /> | ||
| + | [[Datei:Aufgabe 11.5 WiSe 18 19.png|500px]]<br /> | ||
| + | Punkspiegelung der Halbgeraden des Winkels um P, konstruiert durch je einen Kreis mit Radius |P(jeweiliger Punkt)|, die Bildpunkte A',B',C' können dann durch die Schnittpunkte dieser Kreise mit den Geraden (jeweiliger Punkt)P konstruiert werden. Die Schnittpunkte von Winkel und Abbildung des Winkels sind die Punkte D und E, wobie D der Bildpunkt von E ist und somit gilt, dass ED eine Gerade durch P ist und |EP|= |PD|.<br /> | ||
| + | <br /> | ||
| + | Beweis: (Im Beweis ist der Scheitelpunkt C) <br /> | ||
| + | Vor: D<sub>(P,180)</sub>(<math>\angle{ACB}</math>) = <math>\angle{A'C'B'}</math> und <math>\angle{ACB}</math> geschnitten <math>\angle{A'C'B'}</math> = {D;E}<br /> | ||
| + | Beh: P ε <math>\overline{DE}</math> und |DP| = |PE|<br /> | ||
| + | <br /> | ||
| + | 1.) D<sub>(P,180)</sub> = S<sub>p</sub> <math>\circ</math> S<sub>q</sub> '''- Vor; Def. Drehung'''<br /> | ||
| + | 2.) p sei so gewählt, dass gilt: p steht senkrecht auf AC => S<sub>p</sub>(AC) = AC '''- Relative Lage der Spiegelachsen bei Drehungen, AC ist Fixgerade für die Spiegelung an p'''<br /> | ||
| + | 3.) q || AC => S<sub>q</sub>(AC) = A'C' mit q || A'C' '''- 2.) Transitivität der Parallelität, Spiegelung einer Geraden an einer Parallelen erzeugt eine Parallele'''<br /> | ||
| + | 4.) C'A' geschnitten CB = D '''- 3.)''' | ||
| + | 5.) D<sub>(P,180)</sub> (D) = E '''- 2.)'''<br /> | ||
| + | 6.) P ε <math>\overline{DE}</math> und |DP| = |PE| '''- 5.)'''<br /> | ||
| + | Die Behauptung ist bewiesen. --[[Benutzer:CIG UA|CIG UA]] ([[Benutzer Diskussion:CIG UA|Diskussion]]) 22:15, 11. Jan. 2019 (CET)<br /> | ||
| + | <br /> | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Aktuelle Version vom 11. Januar 2019, 22:15 Uhr
- Gegeben sei ein Winkel
und ein Punkt P im Inneren des Winkels der nicht auf einem der Schenkel des Winkels liegt. Konstruieren Sie eine Strecke 
deren Endpunkte D und E jeweils auf einem der beiden Schenkel des Winkels liegen und P Mittelpunkt der Strecke ist.
- Beweisen Sie, dass Ihre Konstruktion richtig ist.
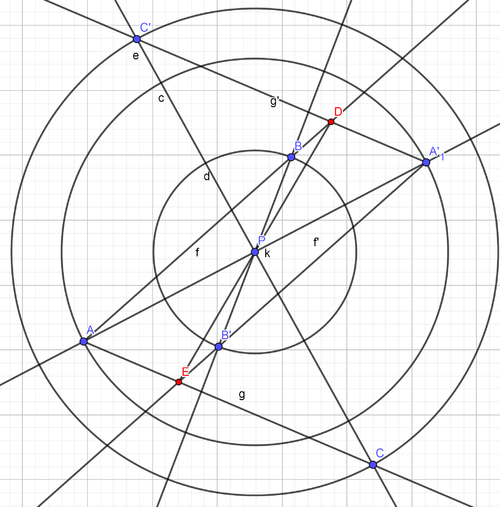
Punkspiegelung der Halbgeraden des Winkels um P, konstruiert durch je einen Kreis mit Radius |P(jeweiliger Punkt)|, die Bildpunkte A',B',C' können dann durch die Schnittpunkte dieser Kreise mit den Geraden (jeweiliger Punkt)P konstruiert werden. Die Schnittpunkte von Winkel und Abbildung des Winkels sind die Punkte D und E, wobie D der Bildpunkt von E ist und somit gilt, dass ED eine Gerade durch P ist und |EP|= |PD|.
Beweis: (Im Beweis ist der Scheitelpunkt C)
Vor: D(P,180)(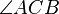
) = 
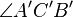und 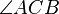geschnitten 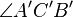= {D;E}
Beh: P ε und |DP| = |PE|
1.) D(P,180) = Sp 
Sq - Vor; Def. Drehung
2.) p sei so gewählt, dass gilt: p steht senkrecht auf AC => Sp(AC) = AC - Relative Lage der Spiegelachsen bei Drehungen, AC ist Fixgerade für die Spiegelung an p
3.) q || AC => Sq(AC) = A'C' mit q || A'C' - 2.) Transitivität der Parallelität, Spiegelung einer Geraden an einer Parallelen erzeugt eine Parallele
4.) C'A' geschnitten CB = D - 3.)
5.) D(P,180) (D) = E - 2.)
6.) P ε und |DP| = |PE| - 5.)
Die Behauptung ist bewiesen. --CIG UA (Diskussion) 22:15, 11. Jan. 2019 (CET)
