Lösung von Aufgabe 12.1P (WS 18/19): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
 
Zeile 11: Zeile 11:
 
<br />
 
<br />
 
<br />
 
<br />
−
1. φ<sub>1</sub> ist eine Verschiebung, φ<sub>2</sub> ist eine Drehung.<br />
+
1. φ<sub>1</sub> ist eine Verschiebung, φ<sub>2</sub> ist eine Drehung.<br /><br />
 +
 
 
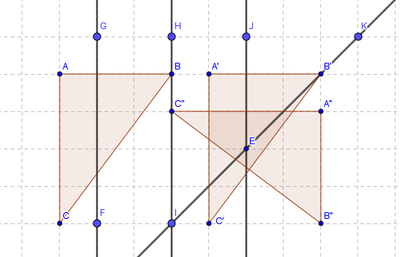
2.[[Datei:Aufgabe 12.1.1 WS 18 19.png|400px]]<br />
 
2.[[Datei:Aufgabe 12.1.1 WS 18 19.png|400px]]<br />
 
φ<sub>1</sub> = FG <math>\circ</math> HI und φ<sub>2</sub> = EJ <math>\circ</math> IK<br /><br />
 
φ<sub>1</sub> = FG <math>\circ</math> HI und φ<sub>2</sub> = EJ <math>\circ</math> IK<br /><br />

Aktuelle Version vom 16. Januar 2019, 21:01 Uhr

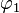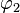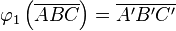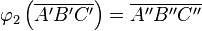Dargestellt ist hier die Nacheinanderausführung zweier Abbildungen \varphi_1 und \varphi_2, mit \varphi_1\left( \overline{ABC} \right) = \overline{A'B'C'} und \varphi_2\left( \overline{A'B'C'} \right) = \overline{A''B''C''}.
Hinweis: Der Punkt E hat eine besondere Bedeutung für 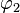\varphi_2.
Falls nichts angezeigt wird, können Sie mit folgendem Link den Servercache leeren.


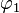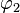  1. Um welche Arten von Abbildungen handelt es sich bei \varphi_1 und \varphi_2?
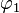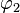  2. Zeichnen Sie jeweils für \varphi_1 und \varphi_2 die passende Anzahl von Spiegelachsen in die Skizze ein.
  3. Wir betrachten nun die Verkettung 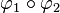\varphi_1\circ \varphi_2 . Durch welche Ersatzabbildung kann diese Verkettung 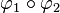\varphi_1\circ \varphi_2 ersetzt werden? (Begründen Sie Ihre Entscheidung).
  4. Zeichnen Sie die Achsen der Ersatzabbildung in die Skizze oben ein. Hinweis: Sie dürfen das Gitter im Hintergrund als Orientierung nutzen.



1. φ1 ist eine Verschiebung, φ2 ist eine Drehung.

2.Aufgabe 12.1.1 WS 18 19.png
φ1 = FG \circ HI und φ2 = EJ \circ IK

3. Eine Drehung. Es gilt: [Annahme: HI verliefe durch E, sodass HI und FG nicht weiter verschoben werden müssen.]
φ1\circφ2 = Sa\circSb\circSc\circSd mit a=FG; b=HI; c=EF; d=IK - Def. Verschiebung und Drehung
= Sa\circSb\circSc'\circSd' mit Betrag " orientierter Winkel cd " = Betrag " orientierter Winkel c'd' " und c' = b - relative Drehbarkeit der Achsen einer Drehung
= Sa\circSd' - Identität b und c'.
a geschnitten d' sei D1, somit ist die gesamte Verkettung reduzierbar auf eine Drehung um D1 um 90.

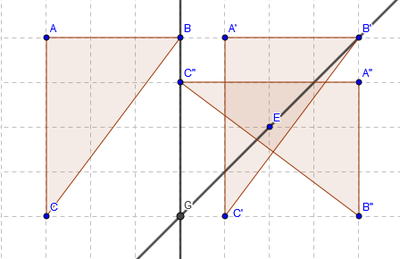
4.Aufgabe 12.1.2 WS 18 19.png
--CIG UA (Diskussion) 21:01, 16. Jan. 2019 (CET)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_12.1P_(WS_18/19)&oldid=32753“