Lösung von Aufgabe 14.3P (WS 18/19): Unterschied zwischen den Versionen
CIG UA (Diskussion | Beiträge) |
CIG UA (Diskussion | Beiträge) |
||
| Zeile 9: | Zeile 9: | ||
4.) |γ<sub>1</sub>| + |α<sub>3</sub>| + |β<sub>3</sub>| = 180 => 180 - |γ<sub>1</sub>| = |α<sub>3</sub>| + |β<sub>3</sub>| und (180 - |γ<sub>1</sub>| = |α<sub>1</sub>| + |β'<sub>1</sub>| und |α<sub>3</sub>| > |α<sub>1</sub>|) => |α<sub>3</sub>| > |β<sub>3</sub>| '''- 1.); 3.); Transitivität der Gleichheitsrelation'''<br /> | 4.) |γ<sub>1</sub>| + |α<sub>3</sub>| + |β<sub>3</sub>| = 180 => 180 - |γ<sub>1</sub>| = |α<sub>3</sub>| + |β<sub>3</sub>| und (180 - |γ<sub>1</sub>| = |α<sub>1</sub>| + |β'<sub>1</sub>| und |α<sub>3</sub>| > |α<sub>1</sub>|) => |α<sub>3</sub>| > |β<sub>3</sub>| '''- 1.); 3.); Transitivität der Gleichheitsrelation'''<br /> | ||
5.) |b<sub>3</sub>| = |b'| = |a<sub>1</sub>| und |a<sub>3</sub>| = |a<sub>1</sub>| + |a<sub>2</sub>| = |CB'| + |B'B| '''- 1.); 3.); 4.)'''<br /> | 5.) |b<sub>3</sub>| = |b'| = |a<sub>1</sub>| und |a<sub>3</sub>| = |a<sub>1</sub>| + |a<sub>2</sub>| = |CB'| + |B'B| '''- 1.); 3.); 4.)'''<br /> | ||
| − | 6.) |a<sub>3</sub>| > |a<sub>1</sub>| => |a<sub>3</sub>| > |b<sub>3</sub>|<br /> | + | 6.) |a<sub>3</sub>| > |a<sub>1</sub>| => |a<sub>3</sub>| > |b<sub>3</sub>|<br /> '''- 5.)''' |
|α<sub>3</sub>| > |β<sub>3</sub>| => |a<sub>3</sub>| > |b<sub>3</sub>|<br /> | |α<sub>3</sub>| > |β<sub>3</sub>| => |a<sub>3</sub>| > |b<sub>3</sub>|<br /> | ||
Die Behauptung ist wahr. --[[Benutzer:CIG UA|CIG UA]] ([[Benutzer Diskussion:CIG UA|Diskussion]]) 20:55, 29. Jan. 2019 (CET) | Die Behauptung ist wahr. --[[Benutzer:CIG UA|CIG UA]] ([[Benutzer Diskussion:CIG UA|Diskussion]]) 20:55, 29. Jan. 2019 (CET) | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Aktuelle Version vom 29. Januar 2019, 20:55 Uhr
Beweisen Sie Satz XIV.2: (Dem größeren Winkel liegt die größere Seite gegenüber)
Vor: |α| > |β|; Beh: |a| > |b|
1.) 
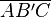mit den Winkeln |α1| = |β'1| und |γ1| mit |α1| = |β'1| => |a| = |b| - Def. gleichschenkliges Dreieck
2.) 
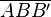mit den Winkeln |α2|, |β'2| und |β2| mit B ε CB' und ZW.(CB'B)
3.) 
mit den Winkeln |α3|, |β3| und |γ3| mit |γ1| = |γ3| und |β3| = |β1| und |α3| = |α2| + |α1| - 1.); 2.); koll.(B,B',C)
4.) |γ1| + |α3| + |β3| = 180 => 180 - |γ1| = |α3| + |β3| und (180 - |γ1| = |α1| + |β'1| und |α3| > |α1|) => |α3| > |β3| - 1.); 3.); Transitivität der Gleichheitsrelation
5.) |b3| = |b'| = |a1| und |a3| = |a1| + |a2| = |CB'| + |B'B| - 1.); 3.); 4.)
6.) |a3| > |a1| => |a3| > |b3|
- 5.)
|α3| > |β3| => |a3| > |b3|
Die Behauptung ist wahr. --CIG UA (Diskussion) 20:55, 29. Jan. 2019 (CET)
