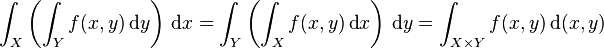GeometrieUndUnterrichtSS2019 04: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „== Vorbereitungsauftrag == Der ''Satz von Fubini'' ist ein Satz über die Möglichkeit der Berechnung von Doppelintegralen durch iterative Integration: :<mat…“) |
(→Vorbereitungsauftrag) |
||
| Zeile 11: | Zeile 11: | ||
# Formulieren Sie den ''Satz von Fubini'' für folgenden Spezialfall: Es sei <math>X \subseteq \mathbb{R}^{n}</math> ein abgeschlossener Quader, und <math>Y \subseteq \mathbb{R}</math> ein abgeschlossenes Intervall. Ferner sei <math>A\subseteq X\times I</math> messbar. Wir betrachten für <math>h\in I</math> die Mengen <math>A(h) = \{ x\in X \mid (x,h) \in A\}</math>. Wie können Sie <math>\int_{A}d(x,y)</math> berechnen? | # Formulieren Sie den ''Satz von Fubini'' für folgenden Spezialfall: Es sei <math>X \subseteq \mathbb{R}^{n}</math> ein abgeschlossener Quader, und <math>Y \subseteq \mathbb{R}</math> ein abgeschlossenes Intervall. Ferner sei <math>A\subseteq X\times I</math> messbar. Wir betrachten für <math>h\in I</math> die Mengen <math>A(h) = \{ x\in X \mid (x,h) \in A\}</math>. Wie können Sie <math>\int_{A}d(x,y)</math> berechnen? | ||
# Für das ''Prinzip von Cavalieri'' findet man in Schulbüchern die unten stehende Formulierung. Verwenden Sie die hier angesprochene Integrationstheorie, um eine fachmathematisch präzise Formulierung zu erstellen. | # Für das ''Prinzip von Cavalieri'' findet man in Schulbüchern die unten stehende Formulierung. Verwenden Sie die hier angesprochene Integrationstheorie, um eine fachmathematisch präzise Formulierung zu erstellen. | ||
| + | # Welche Bestandteile der Schulbuch-üblichen Formulierung entsprechen welchen Bestandteilen der fachmathematisch präzisen Formulierung? | ||
| − | === Das Prinzip von Cavalieri === | + | === Das Prinzip von Cavalieri (für Körper) === |
Zwei Körper haben das gleiche Volumen, wenn sie gleiche Grundflächeninhalte sowie gleiche Höhen besitzen und sämtliche Schnittflächen im gleichen Abstand parallel zur Grundfläche den gleichen Flächeninhalt haben. | Zwei Körper haben das gleiche Volumen, wenn sie gleiche Grundflächeninhalte sowie gleiche Höhen besitzen und sämtliche Schnittflächen im gleichen Abstand parallel zur Grundfläche den gleichen Flächeninhalt haben. | ||
Version vom 18. April 2019, 17:37 Uhr
Inhaltsverzeichnis |
Vorbereitungsauftrag
Der Satz von Fubini ist ein Satz über die Möglichkeit der Berechnung von Doppelintegralen durch iterative Integration:
Bearbeiten Sie die folgenden Aufträge.
- Wiederholen Sie den Satz von Fubini aus Ihrer entsprechenden Mathematik-Vorlesung (vermutlich Analysis, Maßtheorie, Wahrscheinlichkeitstheorie, Funkionalanalysis o.Ä.).
- Formulieren Sie den Satz von Fubini für folgenden Spezialfall: Es sei
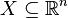 ein abgeschlossener Quader, und
ein abgeschlossener Quader, und 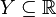 ein abgeschlossenes Intervall. Ferner sei
ein abgeschlossenes Intervall. Ferner sei 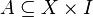 messbar. Wir betrachten für
messbar. Wir betrachten für 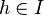 die Mengen
die Mengen 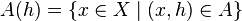 . Wie können Sie
. Wie können Sie 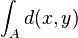 berechnen?
berechnen?
- Für das Prinzip von Cavalieri findet man in Schulbüchern die unten stehende Formulierung. Verwenden Sie die hier angesprochene Integrationstheorie, um eine fachmathematisch präzise Formulierung zu erstellen.
- Welche Bestandteile der Schulbuch-üblichen Formulierung entsprechen welchen Bestandteilen der fachmathematisch präzisen Formulierung?
Das Prinzip von Cavalieri (für Körper)
Zwei Körper haben das gleiche Volumen, wenn sie gleiche Grundflächeninhalte sowie gleiche Höhen besitzen und sämtliche Schnittflächen im gleichen Abstand parallel zur Grundfläche den gleichen Flächeninhalt haben.