GeometrieUndUnterrichtSS2019 03: Unterschied zwischen den Versionen
(→Ergebnisse der Nachbereitung) |
(→Tabelle 1: Arten der Begrifferarbeitung) |
||
| Zeile 37: | Zeile 37: | ||
* Begriffsbildung aus Bildern | * Begriffsbildung aus Bildern | ||
|- | |- | ||
| − | | '''Spezifikation aus einem Oberbegriff''' || Ausbildung eines Teilbegriffs durch Einschränkung von Eigenschaften bzw. Angabe von Anforderungen || allgemeiner Oberbegriff || || | + | | '''Spezifikation aus einem Oberbegriff''' || Ausbildung eines Teilbegriffs durch Einschränkung von Eigenschaften bzw. Angabe von Anforderungen || allgemeiner Oberbegriff || höhere Klassenstufen || |
* Notwendigkeit von Vorwissen | * Notwendigkeit von Vorwissen | ||
* Deduktiver Charakter und nicht von der Problemstellung ausgehend (nicht induktiv) | * Deduktiver Charakter und nicht von der Problemstellung ausgehend (nicht induktiv) | ||
| Zeile 55: | Zeile 55: | ||
* Abstraktionsprozess | * Abstraktionsprozess | ||
* Idealisierungsprozess | * Idealisierungsprozess | ||
| − | || Beispiele und Gegenbeispiele || | + | || Beispiele und Gegenbeispiele || uneingeschränkt || |
* Förderung von Prototypen und Partitionen anstelle von Hierachien (''interner Bezüge'') | * Förderung von Prototypen und Partitionen anstelle von Hierachien (''interner Bezüge'') | ||
|| | || | ||
Version vom 17. Mai 2019, 08:56 Uhr
Inhaltsverzeichnis |
Vorbereitungsauftrag
Entwerfen Sie eine Unterrichtsaktivität für die Einführung bzw. einführenden Erarbeitung des Begriffs Parallelogramm. Ziel der Unterrichtsaktivität ist die Kenntnis der Begriffsdefinition. Gehen Sie von einer generischen (Real-)Schulklasse der sechsten Jahrgangsstufe aus. Gehen Sie davon aus, dass die Schüler*innen aus der fünften Jahrgangsstufe bereits in der Lage sind, 'Parallelität' im Kontext paralleler Geraden und Vierecke, Quadrate und Rechtecke identifizieren können. Beachten Sie auch den gemeinsamer Bildungsplan für die Sekundarstufe I des Landes Baden-Württemberg.
In der Didaktischen Werkstatt Mathematik und Informatik der PH Heidelberg finden Sie u.a. eine Sammlung von verschiedenen Schulbüchern, die Sie gerne zur Inspiration nutzen können.
Sitzungsmaterialien
- Begleitfolien der Seminarsitzung vom 10.05.2019
- Screenshot „Das Problem der Apfelbauern“ (Mittelsenkrechte als Äquidistanzkurve)
Dokumentation der Sitzung
Zusammenfassung
Das Augenmerk dieser Sitzung lag auf der kurzfristigen Erarbeitungsphase von Begriffen. Dabei haben wir die verschiedenen Zugänge zur Erarbeitung von geometrischen Begriffen sowie konkrete Beispiele für sie kennengelernt. Dabei haben sich das operative Prinzip sowie die Begriffsbildung durch Abstraktion als zentral für den Begriffserwerb im Geometrieunterricht in der Sekundarstufe erwiesen. Da sich mathematische Denkstile wie Lernstile auch in persona je nach Thematik und über die Zeit abwechseln und jeder Zugang verschiedene Vor- und Nachteile besitzt, ist ein ergänzender, abwechslungsreicher Umgang der Zugänge am gewinnbringendsten. Unabhängig von dem gewählten Zugang sollten Phänomene als Ausgangspunkt für die Begriffsbildung im Geometrieunterricht genutzt werden und zwar solche, die unter mathematischen und didaktischen Aspekten vertretbar sind.
Inputphase
Im Allgemeinen erfolgt der kurzfristige Erwerb von geometrischen Begriffen in drei Phasen (vgl. Weigand et al. 2018, S. 100f.). In der ersten Phase wird zunächst ein Bedürfnis zur Bildung des Begriffs geschaffen, indem ein passender Problemkontext, möglichst ein Phänomen (s.u.), betrachtet wird. Danach folgt die Phase der Erarbeitung des Begriffs, in der intuitiv gesammelte Begriffsvorstellungen präzisiert sowie Begriffsinhalt und Begriffsumfang konkretisiert werden. Im Unterricht zählen dazu neben der Sicherung im Heft auch schon erste Übungsphasen. Um einen Begriff in seinem Kontext zu verstehen, schließt sich anschließend eine Reflexionsphase an. In dieser werden Prototypen bewertet und der zu lernendn geometrische Begriff in ein Begriffsnetz einsortiert. Welche Umsetzungsmöglichkeiten sich für die ersten beiden Phasen konkret für eine(n) Lehrer(in) ermöglichen und welche Vor- und Nachteile diese beinhalten, wurde im Verlauf der Sitzung näher erörtert.
Phase 2: Erarbeitungsphase
In der unteren Tabelle sind die Ergebnisse des Vorbereitungsauftrags (siehe unten und Abb. 1) den einzelnen Arten der Begriffserarbeitung zugeordnet sowie Vor- und Nachteile aufgelistet. Die größte Bedeutung für die Erarbeitung eines geometrischen Begriffs in der Sekundarstufe besitzt die operative Begriffsbildung, welche auf dem von Aebli 1985 geprägten operativen Prinzip beruht, sowie in der Sek II immer zunehmender die Begriffsbildung durch Abstraktion.
Tabelle 1: Arten der Begrifferarbeitung
| Arten der Begriffserarbeitung | Grundidee | Ausgangspunkt | Klassenstufe | Nachteile | Bsp. (auch Vorbereitungsauftrag) |
| Exemplarische Begriffsbildung | Generalisierung und Bildung ganzheitlicher Vorstellungen (Gestalt, Bild, Aussehen) durch Vergleich von (gemeinsamen) Eigenschaften und Analyse von Bsp. und Gegenbsp. aus dem Alltag | Einzelobjekt/ Einzelfall | Primarstufe und Übergang zur Sekundarstufe |
|
|
| Spezifikation aus einem Oberbegriff | Ausbildung eines Teilbegriffs durch Einschränkung von Eigenschaften bzw. Angabe von Anforderungen | allgemeiner Oberbegriff | höhere Klassenstufen |
|
|
| Konstruktive oder operative Begriffsbildung (funktionales Denken) |
Ausbildung einer dynamischen bzw. flexiblen Begriffsvorstellung durch internalisiertes, zielgerichtetes Handeln (variable Operationen, Transformationen und Konstruktionen) und bewusstes, reflektierendes Beobachten der durch die Handlung aufgezwungen Eigenschaften | reale, virtuelle oder mentale Handlung | uneingeschränkt |
|
* Parallelstreifen
|
| Begriffsbildung durch Abstraktion (prädikatives Denken) |
Begriffsbildung durch (Äquivalenz-)Klassenbildung, d.h. Sortieren anhand charakteristischer Merkmale. Das inkludiert ein:
|
Beispiele und Gegenbeispiele | uneingeschränkt |
|
|
Operatives Prinzip und operative Begriffsbildung
Das Operative Prinzip (vgl. Aebli 1985, Wittmann 1985) ist ein didaktisches Konzept, welches schulische Lern- und Denkprozesse auf internalisiertes Handeln gründet und zumeist bei Problemlöseaufgaben und Phasen des entdeckenden Lernens eingesetzt wird. Ein zentraler Aspekt des Konzepts ist der Begriff der Operation. An konkreten Problemstellungen beginnen in jeglichen Lebensaltern Denkprozesse. Durch zielgerichtete praktische Handlungen (Zeichnen, Konstruieren, Falten, Bewegen) und bewusste Beobachtungen (Varianz, Invarianz, Abhängigkeiten und Beziehungen) können Operationen, Begriffe und Eigenschaften verinnerlicht und Grundvorstellungen aufgebaut werden ('Interiorisation'). Bei einigen Begriffen und Operationen bedarf es einer zusätzlichen Abstraktion der praktischen Handlungen (z.B. die Zahl л durch Umfangsmessungen) sowie einer begrifflichen (Re-)Konstruktion mit Hilfe der Vorkenntnisse der Schüler. Um sich von Prototypen und konkreten Situation zu lösen, werden sie zahlreichen Transformationen unterzogen und aus verschieden Blickwinkeln betrachtet. Schließlich zeigt sich das Ziel und die Produkte des operativen Prinzips sowohl in der Anwendung auf konkreten Handlungssituationen, als auch in der Erkenntnis des Systemcharakters von Operationen und Begriffen.
- Operative (konstruktive) Begriffsbildung: „Ein Begriff wird nach dieser Methode dadurch erschlossen, dass man ein Verfahren zur Konstruktion der unter den Begriff fallenden Objekte angibt und die diesen Objekten durch die Konstruktion aufgeprägter Eigenschaften untersucht" (Wittmann 1985).
In der Praxis sind für den erfolgreichen Einsatz der operativen Begriffsbildung Beobachtungen der SuS durch zielgerichtete Aufgabenstellungen und Hypothesenaufträge zu unterstützen (Folie 9).
- Welche Transformationen sind durchführbar?
- Welche Operationen ermöglicht das Werkzeug?
- Welche Eigenschaften und Beziehungen haben Objekte?
- Welche Wirkung haben Transformationen auf Eigenschaften und Beziehungen?
- Formulierungen von Vermutungen und Begründungen
Phase 1: Darbietung des Problemkontextes
Phänomene
Phänomene sind für die Entwicklung von Begriffsvorstellungen (Konstituierung mentaler Objekte) gut geeignet sowie dazu, um in den ersten Kontakt mit dem zu erarbeitenden Begriff zu treten. Sie eröffnen eine oder mehrere Problemstellungen, die z.T. auch entwicklungsgeschichtlich zur Begriffsdefinition motiviert haben und die die Sinnhaftigkeit der Begriffsbildung hervorheben. Offensichtlich spielt das Vorwissen oder die Vorerfahrung der SuS eine entscheidende Rolle bei der Entwicklung des Begriffsverständnisses. Faltkanten in einem Blattpapier legen beispielsweise die Definition des Begriffs Gerade nahe (weitere Bsp. Folie 13). Dabei sollte für jeden Begriff die Tragfähigkeit des Phänomens unter mathematischen und didaktischen Gesichtspunkten geprüft werden. Als solide erweisen sich kulturhistorisch-genetische Phänomene (z. B. Quadratur des Kreises, Dreiteilung des Winkels), Alltags-/Lebenswirklichkeits-Phänomene (z. B. Flächenberechnung fürs Fliesenlegen, Optimierungsprobleme wie der kürzeste Weg zwischen A und B in Mannheim) und innermathematische Phänomene (z. B. Invarianz des Abstands zweier Parallelen, Klassifikationen von Vierecken). Nach van Hofe sollte ein dem Begriff angemessenes Beispiel/Phänomen gewählt werden.
Arbeitsphase
Äquidistanzkurven wurden in der Arbeitsphase als Beispielphänomen zum Begriffserwerb der Mittelsenkrechten genutzt und untersucht.
- Äquidistanzpunkte sind diejenigen Punkte (der Ebene/des Raumes), die von vorgegebenen geometrischen Objekten den gleichen Abstand haben.
Dieser koordinatenlose Zugang zur Kurvengeometrie bietet einen „historischen“ Einblick in eine Art und Weise Geometrie zu betreiben. René Decartes und Pierre de Fermat entwickelten (unabhängig voneinander) die Koordinatenmethode erst 1637. Dieses Jahr gilt als natürliche Grenze zum Übergang in die „moderne“ Mathematik. Vor Begründung der Koordinatenmethode wurden Kurven etwa als ebene Schnitte räumlicher Figuren (etwa Kegelschnitte), durch punktweise Konstruktion oder durch (gedachte) mechanische Erzeugung mit bestimmten Werkzeugen konstruiert.
Äquidistanzkurven dienen beispielsweise als Ausgangspunkt zur Beschreibung von Parabeln, Kreisen, Mittelsenkrechten und Winkelhalbierenden. Das Phänomen ist demnach kulturhistorisch-genetisch, aber auch innermathmatisch begründet.
Die Problemstellung
„Alice und Bob sind Apfelbauern. Zwei ihrer Apfelbäume stehen nebeneinander. Jedes Jahr streiten sie sich darum, welche Äpfel auf dem Boden von welchem Baum gefallen sind. Ihr Freund Charlie möchte den beiden helfen. Wie können die Äpfel auf die beiden aufgeteilt werden?“ Neben Charlie waren die Bäume von Alices und Bobs sowie einige Äpfel im Geogebra-Applet als Punkte dargestellt. Im Plenum wurden einige mögliche Schülerantworten bezüglich ihrer Fairness diskutiert und mit Geogebra z.T. auch in Kleingruppen ausprobiertund umgesetzt.
Lösungsvorschläge
Neben der Mittelsenkrechten, deren Begriffsinhalt (Eigenschaft: Äquidistanzkurve zweier Punkte) Ziel der Aufgabe darstellte, wurde auch das Zeichnen zweier Kreise mit Mittelpunkt in je einem Baum durch den Punkt Charlie als Lösungsvorschlag genannt. Bei Letzterem lässt sich jedoch ein Apfel keinem der beiden Kreise zuordnen. Ein an die Konstruktion der Mittelsenkrechten angelehnter Vorschlag wäre das Zeichnen zweier Kreise mit Mittelpunkt in je einem Baum durch den Punkt des jeweils anderen Baumes. Die Äpfel in der Schnittmenge sollten dann geteilt werden. Doch auch hier können (zumindest theoretisch) Äpfel auftauchen, die in keinem Kreis liegen.
Bemerkungen und Kritik
Zum einen wurde festgestellt, dass bei sauberer Formulierung der Fragstellung Nachfragen bezüglich der Hangneigung und Höhe der Bäume vorgebeugt werden kann. Zum anderen entscheidet das Zeitbudget, wie offen bzw. angeleitet sie gefasst werden kann. Dabei sollte das Ziel der Aufgabe immer im Blick behalten werden, denn die Fülle an Lösungsmöglichkeiten und ihr Diskussionspotential erfordert viel Zeit, denn Schülerantworten sollten ernst genommen werden.
Außerdem ist dieser Zugang als Einstiegszugang zum Begriffserwerb der Mittelsenkrechten schlecht geeignet, da Begriffe (wenn möglich) immer angelehnt an ihre Etymologie eingeführt werden sollten. Im Falle der Mittelsenkrechten entspricht das der Konstruktion einer Senkrechten durch den Mittelpunkt einer Strecke zwischen A und B.
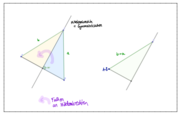
Die SuS wissen i.A. nicht, dass die Mittelsenkrechte weiterhin die Eigenschaft einer Äquidistanzkurve erfüllt. Mit Hilfe der Geogebra-Software, insbesondere des Spurmodus, kann dieser Zugang dazu genutzt werden, dieses Charakteristikum enaktiv zu erschließen und sichtbar zu machen: Dazu wurden die Punkte der Bäume mit dem Punkt Charlie durch eine Strecke verbunden und ihr Abstand durch das Abstandstool gemessen. Die Äquidistanzkurve kann dann bei aktiviertem Spurmodus durch Bewegen von Charlie und konstantes Überwachen der Abstände ermittelt werden. Zu diesen Zeitpunkt ist (den SuS) noch nicht klar, dass die durch den Spurmodus sichtbar gemachte Äquidistanzkurve genau der Mittelsenkrechten der zwei Punkten entspricht. Deshalb steht die Lehrkraft danach vor der Aufgabe beide Zugänge miteinander zu verbinden, um ein integriertes mentales Modell bei den SuS zu produzieren. Dies kann über Plausibilitätsargumente wie Kreise mit Mittelpunkt auf der konstruierten Mittelsenkrechten durch die Ausgangspunkte geschehen oder angelehnt an den eigentlichen Kongruenzbeweis durch Symmetriebetrachtungen eines durch die Mittelsenkrechte geteilten, gleichschenkligen Dreiecks (siehe Abb. 2).
Das Fazit der Arbeitsphase
Zur Untersuchung von Äquidistanzkurven ist die „Spurmodus“-Funktion in Geogebra (auch bei anderen dynamischen Geometrie-Programmen) sehr geeignet.
Zusatzmaterial
Als zusätzliche Übungsgelegenheit für die Unterstützung des Begriffslernens mit Blick auf das Operative Prinzip finden Sie die Aktivität „Schwarze Kisten am Dreieck“ in der GeoGebra.org-Gruppe des Seminars. Entwerfen Sie hierzu ein Arbeitsblatt zur angeleiteten Exploration des Applets. Versuchen Sie dabei explizite Handlungs-, Beobachtungs- und hypothesengenerierende Anweisungen zu geben.
Nachbereitungsauftrag
Entwerfen Sie eine Prüfungsfrage bzw. ein kurzes Prüfungsgespräch zu den Sitzungen zum Begriffslernen (I+II). Ihre Frage sollte dabei nicht nur bloße Wissensabfrage sein, sondern auch Anwendungen, Begründungen oder Diskussionen erfordern. (Sollte Ihnen doch nur Aufgaben zur bloßen Wissensabfrage einfallen, entwerfen Sie drei Prüfungsfragen.)
- Formulieren Sie Ihre Prüfungsfrage bzw. den Anlass für das Prüfungsgespräch in der Aufgabenstellung-Spalte.
- Beschreiben Sie ausführlich, wie mögliche (richtige) Antworten auf Ihre Frage aussehen könnten bzw. welche Aspekte in einem Prüfungsgespräch zu dieser Frage angesprochen werden sollten. Tragen Sie dies entsprechend in die Erwartungshorizont-Spalte ein.
- Erläutern Sie kurz, warum Sie diese Aufgabe einen zentralen Aspekt der Sitzung abdeckt und welche Anforderung an Wissen/Kompetenzen die Aufgabe fordert.
Unter den übergreifenden Literaturhinweise sind insbesondere relevant:
- Kapitel 5 „Begriffslernen und Begriffslehren“ in Weigand et. al. (2018). „Didaktik der Geometrie für die Sekundarstufe I“
- Diverse Ausgangspunkte zu Diskussionen über Grundvorstellungen und Darstellungen sind in den ersten Kapiteln von Ludwig et. al. (2015). „Geometrie zwischen Grundbegriffen und Grundvorstellungen“ zu finden.
- Kapitel 4 in Kaenders & Schmitt (2014). „Mit GeoGebra mehr Mathematik verstehen“ bietet Ausgangspunkte zur Diskussion über das Operative Prinzip. Genauso Wittmann (1985): „Objekte-Operationen-Wirkungen: Das operative Prinzip in der Mathematikdidaktik“ In Mathematik lehren.
Mögliche Inspiration können Sie gerne auch weiteren Quellen entnehmen. Zum Beispiel:
- Mason (2009). „The van Hiele levels of geometric understanding.“ In Colección Digital Eudoxus 1.2.
Ergebnisse der Nachbereitung
Tragen Sie die Ergebnisse Ihrer Nachbereitung in die folgende Tabelle ein.
| Aufgabenstellung | Erwartungshorizont | Diskussion |
|---|---|---|
|
Aus algebraischer Sicht ist die folgende Gleichungskette offensichtlich wahr (Assoziativgesetz für Brüche):
|
Die Symbole lassen sich als Formel für die Berechnung des Flächeninhalt eines Dreiecks interpretieren. In ihnen sind sogar verschiedene Beweisideen der Berechnungsformel enthalten, die sich aus der Berechnungsformel des Flächeninhalts des Rechtecks herleiten lassen: Der Flächeninhalt ist das Produkt der Hälfte der Grundseite mit der Höhe bzw. die Hälfte des Produkts aus Grundseite und Höhe bzw. das Produkt der Grundseite mit der Hälfte der Höhe. Anfertigung von Skizzen zu den jeweiligen Interpretationen. Der geometrische Zugang unterstützt das Aufbauen von Grundvorstellungen zur Bruchrechnung (u.a. Multiplikation Zahl-mal-Bruch und Bruch-mal-Zahl) und zum Termbegriff (u.a. Kalkülvorstellung, Gegenstandsvorstellung, Terme als „Bauplan“?). Aufzählung der Aspekte von Grundvorstellungen. Die Diskussion der Gleichungskette aus geometrischer Perspektive verlangt mindestens ein integriertes Begriffsverständnis von Viereck und Dreieck (van-Hiele: 3 Apstraction). Beziehungen zwischen den Figuren Dreieck und Viereck müssen erkannt werden (Begriffsnetz). Schlussfolgerungen finden vermutlich auf informeller Ebene statt (etwa Zerlegungen und Verschiebungen vs. formaler Nachweis der Kongruenz von Teildreiecken und Flächengleichheit kongruenter Dreiecke). Es werden u.a. die folgenden geometrischen Konzepte angesprochen: Strecke, Rechteck, Dreieck, Streckenlänge, Flächeninhalt, Zerlegungsgleichkeit, Translationsinvarianz von Streckenlänge und Flächeninhalt. |
Die Aufgabe bietet Anlass, das Wissen zu folgenden Inhalten abzufragen: Grundvorstellungen, Stufen des Begriffserwerbs (van-Hiele-Modell). Darüber hinaus wird die Anwendung des Stufenmodells gefordert und es ist eine Begründung für die Stufenzuteilung nötig. |
|
Betrachten Sie die folgende Situation: Für seine Mathematikhausaufgaben dividiert Lukas die Zahl 3 durch 1/3. Er wendet die Rechenregeln zur Bruch-Division richtig an und erhält das Ergebnis 9. Lukas fragt sich: „Warum kann das Ergebnis der Division größer sein als der Dividend?“ 1. Wie erklären Sie sich Lukas‘ Denkfehler? Beziehen Sie das Konzept der Grundvorstellungen in die Beantwortung ein. 2. Mit welchem veranschaulichenden Beispiel könnte diesem Denkfehler entgegen gewirkt werden? 3. Könnte man Lukas den Sachverhalt auch anhand von geometrischen Figuren erklären? |
1. Das Problem zeigt, wie wichtig neben den Rechenverfahren auch inhaltliche Vorstellungen mathematischer Inhalte, wie z.B. der Division, sind. Diese inhaltlichen Vorstellungen werden in der Mathematikdidaktik als Grundvorstellungen bezeichnet. Sie beschreiben die möglichst konkrete, inhaltliche ‚Interpretation‘ von mathematischen Objekten und Sachverhalten und sollen dabei helfen, ein tieferes Verständnis der mathematischen Verfahrensweisen zu erhalten. Lukas verfügt nicht über ausreichende Grundvorstellungen der Division durch Brüche, weil er auf die Vorstellung der Division als ‚Verteilen‘ fixiert ist. Würde er sich stattdessen die Frage stellen, wie oft 1/3 in 3 ‚passt‘, und die Division damit als Frage des richtigen Aufteilens interpretieren, wäre sein Vorstellungsproblem gelöst. 2. Um Lukas‘ Denkfehler vorzubeugen, müsste bei den SuS die Grundvorstellung der Division als ‚Aufteilen‘-Operation geweckt werden. Zur Veranschaulichung des Sachverhaltes eignet sich beispielsweise die folgende Problemstellung: „3 Liter Apfelsaft sind in 1/3-l-Flaschen umzufüllen. Wie viele Flaschen werden hierfür benötigt?“ 3. Die folgende Möglichkeit bietet sich dazu an, Lukas den Sachverhalt bzw. die Grundvorstellung der Division als ‚Aufteilen‘-Operation anhand von geometrischen Figuren zu vermitteln: Gegeben seien 3 identische, geometrische Figuren (z.B. Kreise, Rechtecke, Quadrate), die von den SuS in jeweils 3 gleich große Teile zerlegt werden sollen. Anschließend kann gezählt werden, wie viele ‚Drittel‘ in die 3 Figuren 'passen'. |
Die Aufgabe eignet sich dazu, das didaktische Konzept der 'Grundvorstellungen' anwendungsorientiert abzufragen. |
|
Situationen Einführung gleichseitige und gleichschenklige Dreiecke über AB mit 12 bis 16 Bildern entsprechender Dreiecke und dem Arbeitsauftrag mithilfe eines Lineals die Bilder in zwei Kategorien einzuteilen. Fragen: 1. Welche Art von Begriffserarbeitung wurde hier gewählt und wieso? Gibt es Kritik an dieser Art? 2. Ist diese Art typisch bzw. geeignet um in der Sek. I einen Begriff einzuführen? 3. Welche Stufe den van-Hiele-Modell wird mit dieser Begriffseinführung angesprochen? |
1. Begriffserarbeitung durch Abstraktion von gegebenen Objekten. Begriffsbildung wird als Klassenbildung verstanden anhand der charakteristischen Merkmale der Objekte (2 oder 3 gleich lange Seiten). Der Arbeitsauftrag „sortiere die Figuren nach ihrer Form“ ist typisch für diese Art der Begriffserarbeitung. Kritik: Überbetonung Unterschiede, hauptsächlich bildliche Vorstellungen 2. Typisch für Sek. 1, da nur Konstruktiv-operative Begriffsbildung oder Begriffsbildung durch Abstraktion zentral sind. 3. Analyse- Stufe, da es um die Klassifizierung von Dreiecke und dem Erkennen und Beschreiben von deren Eigenschaften geht. Diese Eigenschaften begründen Klassifizierung. Inhaltliches Begriffsverständnis, da noch keine Beziehung zwischen Eigenschaften hergestellt wird (vgl. Abstraktion). |
Es werden die im Seminar besprochenen Konzepte des Begriffslernens und der Begriffserarbeitung angesprochen und abgefragt. |
|
Betrachten Sie die Einführung des Begriffs eines Parallelogramms. Suchen Sie sich einen möglichen Einstieg einer Unterrichtsstunde aus (z.B. Parallelstreifen, Arbeitsblatt mit verschiedenen Vierecken,…), in welcher der Begriff des Parallelogramms eingeführt werden soll und beschreiben Sie anhand des Van-Hiele Modells den schrittweisen Begriffslernprozess in den entsprechenden 5 Phasen. |
Beispiel Parallelstreifen: 1. Visualisation: Vierecke werden gelegt und dadurch eine ganzheitliche Erfassung von dem geometrischen Objekt des Vierecks angeregt. Basale Kenntnisse (4 Ecken, 4 Seiten,..) werden aktiviert. 2. Analysis: Spezielle Eigenschaften (verschiedene Winkelgrößen, Seitenlängen,..) werden erkannt und beschrieben. 3. Abstraction: Klassifizierungen (Rechteck, Quadrat, Parallelogramm) werden verstanden und mathematische Definitionen der einzelnen Begriffe herausgearbeitet. 4. Deduction: Geometrische Theorien und Eigenschaften der speziellen Kategorien Quadrat, Rechteck, Parallelogramm werden erkannt und Beziehungen zwischen den Begriffen werden schlussgefolgert. 5. Rigor: wird in der Schule eher weniger praktiziert. Das Verständnis von Beweisen und anspruchsvollen Sätzen ist in der Schule nicht zwingend gegeben. |
Durch diese Aufgabe wird das Van-Hiele Modell wiederholt und der Prozess des Begriffslernens anhand des Beispiels eines Parallelogramms nachvollzogen. Eigenschaften und Beziehungen geometrischer Objekte werden gefordert und man versetzt sich in eine konkrete Unterrichtseinheit. |
|
Eine siebte Klasse bearbeitet die folgende Aufgabenstellung: Wie viele gemeinsame Punkte kann eine Kreislinie mit einer Geraden haben? Treten hierbei Symmetrien auf? (Wie) Ist es möglich eine Gerade zu konstruieren, welche genau einen gemeinsamen Punkt mit der Kreislinie besitzt?
|
Es werden u.a. die folgenden geometrischen Konzepte angesprochen: Gerade, Kreis, Passante, Sekante, Tangente, rechte Winkel, Orthogonale und Achsensymmetrie. Die Lösung der Aufgabenstellung verlangt mindestens ein Begriffsverständnis auf der Stufe 3 Apstraction (van Hile). Beziehungen zwischen Gerade und Kreis müssen erkannt werden. Schlussfolgerungen bezüglich der Konstruktion der Tangenten finden vermutlich nur auf informeller Ebene statt. (Es sieht so aus, als steht die Tangente senkrecht zum Radius durch den Schnittpunkt.) In der Sekundarstufe 1 sind die konstruktiv-operative Begriffsbildung bzw. die Begriffsbildung durch Abstraktion zentral. Eine mögliche Vereinfachung der Aufgabenstellung könnte wie folgt aussehen: Die Klasse experimentiert nicht selbst mit der Anzahl der gleichen Punkte, sondern es werden die drei Möglichkeiten vorgegeben und dann selbstständig genauer auf ihre Eigenschaften untersucht. |
Die Aufgabe eignet sich dazu, die Einführung geometrischer Konzepte aus einer Aufgabenstellung in den Kontext des Stufenmodells der Begriffsbildung zu übertragen. Desweiteren wird bewertet, welche Arten der Begriffsbildung in welcher Klassenstufe sich als sinnvoll erweißen. |
|
Im Untericht wurde anhand von Prototypen, mit unterschiedlich großen benachbarten Winkeln und Seiten, der Begriff des Parallelograms erarbeitet. Die anschließende Reflexionsphase zeigt bei einigen SuS. Probleme beim erkennen von Quadraten, Rechtecken, Rauten usw. als Parallelograme.
|
Im Kern beruht die Problematik auf der Vorstellung Parallelograme seien immer schief. Dabei herrscht eine Inuitive, ganzheitliche Vorstellung vor, die unzureichende Verknüpfungen oder Abgrenzungen zu den Begriffen Quadrate, Rechtecke, Raute aufzeigt. Zum Abbau der Fehlvorstellung kann ein Konflikt zum Präkonzept Parallelograme erzeugt werden. So lassen sich durch systematische Erkundung der Eigenschaften von schiefen Parallelogramen, Quadraten usw. Gemeinsamkeiten und Unterschiede finden, die in den SuS. ein kritische Prüfung ihrer Präkonzepte anregen. So festigt sich eine Inhaltliche Vorstellung. Über Gemeinsamkeiten der Begriffe lässt sich der Parallelogramsbegriff in des Begriffsnetz der Vierecke einordenen und so ein Integrierte Begriffsvorstellung erzielen. |
Es werden beispielhaft Erarbeitung und Reflexion des Kurzfristigen Lehren geometrischer Begriff abgefragt.
|
|
Eine Lehrerin in Klasse 5 führt den Begriff des Drachenvierecks ein, indem sie die SuS ein DIN A5 Blatt zu einem DIN A6 Blatt falten lässt. Danach sollen die SuS mit der Schere zwei Schnitte legen, die zusammen mit der Faltkante ein Dreieck ergeben. Anschließend wird auseinander gefaltet.
|
Die Lehrerin wählt eine operative bzw. konstruierende Begriffserarbeitung, welche auf dem Operativen Prinzip beruht. Die Schüler sollen durch den enaktiven Zugang zu einer dynamischen Begriffsvorstellung von Drachen gelangen. Durch die (aufgrund der Klassengröße mehrfach) durchgeführte Konstruktion (falten und schneiden) wird dem Objekt Eigenschaften und Beziehungen aufgeprägt, sodass sich SuS den Begriffsinhalt und durch mehrfaches Durchführen auch den Begriffsumfang relativ selbständig erschließen können. Eine Prototypenfixierung und eine Verkümmerung der feinmotorischen Fähigkeiten kann dadurch auch entgegengewirkt werden. Die Lehrkraft kann die Konstruktion vor der Klasse vormachen, sodass auch ohne Sprache jeder SuS die Möglichkeit hat aktiv das zu untersuchende Objekt zu erforschen (-> Inklusion). Außerdem können Beziehungen zu anderen Begriffen (Raute, Quadrat) beobachtet werden, die den zu erlernenden Begriff an ein schon vorhandenes Begriffsnetz anknüpft. Wichtig bei dem gewählten Zugang ist nicht nur das zielgerichtete, internalisierte Handeln, sondern auch das bewusste Beobachten der Wirkung der Operation. Die Lehrerin sollte/kann dies durch einige der folgenden Leitfragen unterstützen:
Alternativ könnte man auch eine Sortierungsaufgabe stellen, in der Drachenvierecke aus verschiedenen Vierecken ausgesucht werden sollen (Begriffsbildung durch Abstraktion). Ein anderer Zugang wäre ein „echter“ Drache, an dem Eigenschaften untersucht werden (Exemplarische Begriffsbildung) oder die Definition eines Drachen als ein bzgl. einer Diagonale achsensymmetrisches Viereck (Spezifikation aus einem Oberbegriff). Grundsätzlich ist für eine umfassende Begriffsvorstellung der Einsatz verschiedener Zugänge am besten. |
Diese Aufgabe deckt die verschieden Arten der Begriffserarbeitung, insbesondere das Operative Prinzip ab. An Hand der operativen Begriffserarbeitung werden Herausforderungen, Vorteile, Nachteile sowie Alternativen diskutiert und reflektiert. Ausgehend von dieser Frage lassen sich weiter Fragen zu den Phasen des kurzfristigen Begriffserwerb, Grund- bzw. Fehlvorstellungen oder mentalen Modellen stellen. |
|
Der Lehrplan der 5. Klasse (Gymnasium) sieht vor, dass neben den Begriffen Viereck, Rechteck und Quadrat auch die Begriffe Würfel und Quarder eingeführt werden. Darüber hinaus wird gefordert, den SuS die Darstellungsform des Würfel- bzw. Quardernetzes zu vermitteln und Zusammenhänge zu anderen Darstellungsformen herzustellen (z.B. zu Schrägbildern). 1) Wie beurteilen Sie dieses Vorgehen? Welche Schwierigkeiten können bei der Realisierung im Unterricht auftreten und wie ließen sich diese beheben? 2) Welche Aspekte des Begriffslernens werden bei einem solchen Ansatz besonders angesprochen? 3) Welche Arten des Begriffslernens lassen sich an diesem Ansatz realisieren? Nennen Sie Beispiele! |
1)
2)
3)
|
|
|
Eine klassische Methode zur Konstruktion von Kreisen ist das zeichnen von Kreisen mit Hilfe einer Schnur. Ein Ende der Schnur wird dabei beispielsweise mit einer Stecknadel fixiert, während ein Stift/Stück Kreide am anderen Schnurende befestigt wird. Die Schnur wird gespannt und der Stift um den Mittelpunkt geführt, um einen Kreis zu zeichnen. Sie beschließen den Begriff des Kreises auf diese Art und Weise einzuführen. 1) Welche Art der Begriffsbildung liegt dieser Methode zu Grunde? 2) Wie lautet die formale Definition des Kreises? Welche inhaltlichen Aspekte des Begriffs Kreis lassen sich durch die gewählte Handlung ableiten? 3) In welcher Phase des Begriffslernens nach dem van-Hiele-Modell würden Sie einen solchen Ansatz wählen? |
1) Das operative Prinzip liegt der Methode zu Grunde. Eine konstruktive oder operative Art der Begriffsbildung wird hier gewählt. Durch die Handlung werden inhaltliche Eigenschaften internalisiert. Schülerinnen und Schüler lernen den Begriff Kreis zu denken, indem sie die definierenden Eigenschaften eines Kreises in der realen Welt umsetzen ("Denken ist internalisiertes Handeln" - Piaget). 2) Def.: Menge aller Punkte, welche im Abstand r>0 zu einem Punkt P liegen. Bei der Konstruktion von Kreisen mit der gegebene Methode lassen sich die folgenden inhaltlichen Eigenschaften von Kreisen nachvollziehen:
Die direkten Analogien zwischen Konstruktionswerkzeugen und Kreiseigenschaften machen den Begriff und die abstrakte Definition des Kreises greifbar. 3) Der Ansatz lässt sich in der zweiten Phase des Begriffslernens nach van-Hiele zuordnen (2. Analysis: Geometrisch-analysierendes Denken). Denn:
|
|
Literaturhinweise
- Wittmann (1985): „Objekte-Operationen-Wirkungen: Das operative Prinzip in der Mathematikdidaktik“ In Mathematik lehren.
- Aebli (1985): „Das Operative Prinzip“ In Mathematik lehren. (Zweiter Teil des PDFs)
- Schwank (2003): „Einführung in prädikatives und funktionales Denken“ In ZDM Mathematics Education
- Scriba und Schreiber (2010): „5000 Jahre Geometrie“.


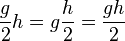 .
.

